Знайти значення виразу :
√(√6-3)²+√(2-√6)²
Другие вопросы по теме Алгебра
Популярные вопросы
- Анализ стиха муза ахматовой...
2 - На праздник пришло всего 45 ребят.В весёлых соревнованиях участвовали...
3 - Нехай х1 і х2 корені рівняння x^2+5x-13=0; Знайдіть х1^2+х2^2 .Самі...
2 - После строительства дома осталось некоторое количество плиток. Их...
3 - Образуйте от глаголов данных в скобках, Participle II. Полученные...
2 - Як і чому змінилися взаємини між мешканцями лісової хатини? Як ці...
3 - Инженерная графика Упражнение 46 - Вариант 01 Вал Скиньте проект...
1 - Образуйте от данных глаголов две формы ParticipleI. Полученные причастия...
1 - Чому ХІ-Іхст в Греції називають гомерівським періодом або темним...
3 - Встановіть відповідність між назвами оргпнізмів та їх приналежністю...
1
1
Объяснение:
Выражение в принципе можно понять двумя Первый более вероятен:
По определению,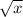 - такое неотрицательное число, квадрат которого равен
- такое неотрицательное число, квадрат которого равен  . Это выражение определено только для
. Это выражение определено только для 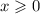 . Отсюда получается, что
. Отсюда получается, что 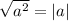 : и
: и 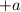 , и
, и 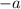 дают в квадрате
дают в квадрате 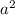 , но подходит только тот, что неотрицателен.
, но подходит только тот, что неотрицателен.
Поскольку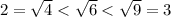 , то
, то  ,
, 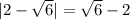 и
и
Второй вариант понимания вряд ли подходит:
не определено, поскольку оба подкоренных выражения отрицательны