1. Алгебра
  2. Знайти восьмий член геометричної

Знайти восьмий член геометричної прогресії (bn), якщо b1=162і b3=18.
Чому дорівнює шостий член геометричної прогресії, якщо b1=81, a q=-1\3

zhenyakulakova zhenyakulakova    2   02.05.2020 20:17    0

Ответы
zippops zippops  14.10.2020 06:07

Перша задача

Знайдемо другий член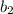 b_2. Від дорівнює середньому геометричному сусідніх членів, взятому зі знаком плюс або мінус (бо прогресія може бути як звичайна, так і знакозмінна):

b_2=\pm \sqrt{162 \cdot 18}=\pm \sqrt{2916}=54

b_2=\pm \sqrt{162 \cdot 18}= \pm \sqrt{2916} = \pm 54

Знайдемо знаменник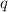 q:

q=\dfrac{b_2}{b_1}=\dfrac{\pm 54}{162}=\pm \dfrac{1}{3}

Знайдемо восьмий член:

b_8=b_1q^7=81 \cdot \left( \pm \dfrac{1}{3}\right)^7=\pm \dfrac{81}{2187}=\pm \dfrac{1}{27}

Друга задача

Обчислимо за формулою:

b_n=b_1q^{n-1}\\b_6=81 \cdot \left(-\dfrac{1}{3}\right)^5=-\dfrac{81}{243}=-\dfrac{1}{3}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Невидимка003 Невидимка003  30.04.2020 20:17
В эксперименте бросаются 3 игральных кубика. Найдите отношение вероятности того, что сумма очков, выпавших на кубиках, больше 15 и вероятности того, что сумма очков, выпавших...
lera10u lera10u  30.04.2020 20:17
Із цифр 3,4,5,6,7 складіть всі можливі 3значні числа, в яких: 1) Цифри не повторюються 2) Цифри повторюються....
mrgebil mrgebil  30.04.2020 20:17
Найдите значение функции y=7x-1при значение аргумента, равно 4...
Аааоо0 Аааоо0  30.04.2020 20:17
А) -3 ∫ ¹(х²+4х+6)dx б) 0 ∫ пи 2 сверху cos² x второй dx Типа номер 2: Неравенство (4х-6)√х²+4≥0 номер 5(г): г) (2х-3)√3х²-5х...
vcurakina vcurakina  30.04.2020 20:17
Розв язати графічно систему рівнянь: У=2 3х-у=4...
andreyderdi159 andreyderdi159  30.04.2020 20:17
Ви тупие нахера блокируете во...
afa2004 afa2004  30.04.2020 20:18
Значення аргумента, при якому значення функції дорівнює 1...
kitkinausmaeva1 kitkinausmaeva1  30.04.2020 20:18
Розвяжіть графічно рівняння 8/х=х-7...
Ecli Ecli  30.04.2020 20:18
Под каким углом график функции y=sin3x/√3 пересекает вначале координат ось абсцисс...
Евгениямагическая Евгениямагическая  30.04.2020 20:18
Реши систему уравнений {10x−3y=2−4x+2y=20 {x= y= (Результаты округли до сотых, если это необходимо умоляяя (((...

Популярные вопросы