Знайти sn якщо bn=8 q=6 b1=3​

9,4

1) Sn= (bn×q-b1)/(q-1) - универсальная формула геометрической прогрессии

2) Подставляем значения

Sn= (8×6-3)/(6-1) = 47/5 = 9,4

Так как номер n при вычислении не получился натуральным числом, то геометрической прогрессии с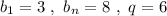    не существует и невозможно найти сумму n членов прогрессии.