1. Алгебра
  2. Знайти 4 числа що утворюють прогресію

Знайти 4 числа що утворюють прогресію перший член якої менший за третій на 24 а другий більший від четвертого на 8

Mixachu Mixachu    1   10.03.2019 09:20    2

Ответы
MorficTV MorficTV  24.05.2020 15:49

Составим уравнения согласно условию

\rm b_1=b_3-24\\ b_2=b_4+8

Используем n-ый член геометрической прогрессии: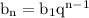 \rm b_n=b_1q^{n-1}, имеем


\rm \displaystyle \left \{ {{b_1=b_1q^2-24} \atop {b_1q=b_1q^3+8}} \right.~~~\Leftrightarrow~~~\left \{ {{b_1(1-q^2)=-24} \atop {b_1(1-q^2)q=8}} \right.~~~\Leftrightarrow~~~ -24q=8\\ \\ q=-\dfrac{1}{3};~~~~b_1=\dfrac{24}{q^2-1}=\dfrac{24}{\bigg(-\dfrac{1}{3}\bigg)^2-1}=-27

Найдем остальные три член геом. прогрессии:

\rm b_2=b_1q=-27\cdot\bigg(-\dfrac{1}{3}\bigg)=9\\ \\ b_3=b_1q^2=-27\cdot\bigg(-\dfrac{1}{3}\bigg)^2=-3\\ \\ b_4=b_1q^3=-27\cdot\bigg(-\dfrac{1}{3}\bigg)^3=1



ответ: -27; 9; -3; 1.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
sergazinaaidana1 sergazinaaidana1  22.04.2020 13:20
Вариант балов 1. Преобразуйте в многочлен:а) (у – 4)2; б) (7х + а)2; в) (5с – 1) (5с + 1);г) (3a + 2b) (3a – 2b).2. У выражение (a – 9)2 – (81 + 2a).3. Разложите на...
ged95 ged95  22.04.2020 13:20
Кто подскажите Кто Желаю здоровья вашим близким родным! Умоляю! ​...
vikasm2001 vikasm2001  22.04.2020 13:20
Доведіть, що значення виразу АЛГЕБРА 7 КЛАСС...
POULINACAT POULINACAT  22.04.2020 13:20
1. Решите уравнение: 13(х-1) - 4(х+2) = 6х - 1, для этого: а) раскройте скобки; б) члены, содержащие х перенесите в левую часть уравнения, а свободные члены – в правую;...
джем16 джем16  22.04.2020 13:20
Вкладник поклав до банку 8000 грн під певний відсоток річних. через рік із рахунку він зняв 1040 грн. Ще через рік на рахунку стало 8208 грн. Скільки відсотків нараховує...
Салатикус Салатикус  22.04.2020 13:21
Решите неравенство 4х^2+х 2х^2+3...
bilpi bilpi  08.04.2020 16:29
Построй график функции y=(x4−41⋅x2+400)/(x−5)⋅(x+4) и определи значения c, при которых прямая y=c имеет с графиком одну общую точку. Если значений несколько, укажи их...
shantropa33 shantropa33  08.04.2020 16:29
Решите биквадратное уравнение 2х^2-3х+7=0. -3х^2+4х-1=0...
балуева2007 балуева2007  08.04.2020 16:29
Представь квадрат двучлена в виде многочлена:(1/4z⁵−7/8)²(Переменную вводи с латинской раскладки.) ​...
pech228 pech228  08.04.2020 16:29
Знайти суму коренів квадратного рівняння :3x квадраті +5x+2=0...

Популярные вопросы