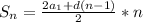знайте суму двадцяти перших членів арифметичної прогресії, якщо сума п'ятого і восьмого члена прогресії дорівнює 82, а сума третього і дев'ятого членів прогресії дорівнює 76
Другие вопросы по теме Алгебра
Популярные вопросы
- _ интерпретация, или четкое, ясное и однозначное описание тех понятий,...
3 - Потребность - это нужда, принявшая специфическую форму в соответствии...
3 - Структурными компонентами плана _ исследования выступают его этапы...
2 - Концепция _ маркетинга основана на планировании, разработке и внедрении...
3 - Функции _характера — это процессы, связанные со сменой стоимости,...
3 - К _ факторам, которыми определяется лояльность торгового посредника...
2 - Под _понимается система управления производственно-сбытовой деятельностью,...
3 - _ признается договор, заключенный организацией и устанавливающий ее...
2 - _ раздел плана социологического исследования включает в себя; формулировку...
2 - _— это вид отношений между рыночными субъектами, когда одна сторона...
2
1)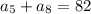
2)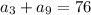
3)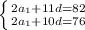
Вычтем:
4)