Знайдіть усі значення параметра а, при яких рівняння logx (ax-4)=2 має єдиний розв‘язок
Другие вопросы по теме Алгебра
Популярные вопросы
- Укажите химические элементы (не менее пяти), атомы которых входят...
3 - Как бы вы разделили смесь сахара, песка и древесных опилок? Составьте...
1 - Чем различаются между собой вещества, смесь которых можно разделить:...
3 - Можешь ли ты своей личной целью признать общую цель изучения...
2 - Однородная или неоднородная смесь образуется при смешивании воды...
1 - Прочитай план действий, который художник составил для себя. 1)...
3 - По-твоему, можно ли считать волшебную палочку в сказках средством...
1 - Приведите по пять примеров известных вам однородных и неоднородных...
3 - Какие свойства веществ называются химическими? Приведите примеры...
2 - Почему медь используется для изготовления электрических проводов?...
3
(см. объяснение)
Объяснение:
ОДЗ:
Заметим, что для любого корня уравнения вне зависимости от значения параметра произведение
произведение 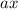 будет больше или равно 4.
будет больше или равно 4.
Причем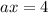 , если
, если 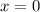 - корень уравнения. Но это невозможно, так как при
- корень уравнения. Но это невозможно, так как при 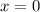 имеем
имеем 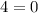 (неверно) при любом значении параметра.
(неверно) при любом значении параметра.
Тогда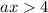 , то есть условие ОДЗ
, то есть условие ОДЗ  будет выполнятся всегда.
будет выполнятся всегда.
Исходное уравнение будет иметь ровно один корень, либо если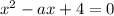 имеет один корень, удовлетворяющий ОДЗ, либо если это уравнение имеет два корня, только один из которых удовлетворяет ОДЗ.
имеет один корень, удовлетворяющий ОДЗ, либо если это уравнение имеет два корня, только один из которых удовлетворяет ОДЗ.
Рассмотрим первый случай. Он достижим, когда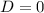 .
.
При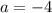 уравнение имеет корень
уравнение имеет корень  , поэтому такое значение параметра не подходит.
, поэтому такое значение параметра не подходит.
При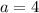 уравнение имеет корень
уравнение имеет корень 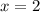 , поэтому такое значение параметра подходит.
, поэтому такое значение параметра подходит.
Рассмотрим второй случай. Он достижим, когда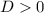 .
.
Здесь также важно, чтобы уравнение либо имело один корень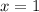 , а другой положительный, либо один корень неположительный, а другой положительный, не равный единице.
, а другой положительный, либо один корень неположительный, а другой положительный, не равный единице.
Обратимся к первой ситуации:
В этом случае уравнение имеет корни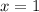 или
или 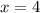 , первый из которых, отпадая, обеспечивает наличие единственного корня у исходного уравнения. Тогда такое значение параметра подходит.
, первый из которых, отпадая, обеспечивает наличие единственного корня у исходного уравнения. Тогда такое значение параметра подходит.
Для того чтобы вторая ситуация могла быть достижимой, необходимо, но не достаточно, чтобы выполнялось условие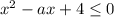 при
при 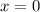 . Однако это невозможно, поэтому такой вариант рассматривать дальше не будем.
. Однако это невозможно, поэтому такой вариант рассматривать дальше не будем.
Итого при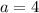 или
или  исходное уравнение имеет единственное решение.
исходное уравнение имеет единственное решение.
Задание выполнено!