Знайдіть суму всіх натуральних чисел, які кратні числу 6 і не перевищують числа 540
Другие вопросы по теме Алгебра
Популярные вопросы
- Якими методами влада управляла суспільством Греції...
2 - Укажите дыхательную систему позвоночных артерии,бронхи,трахея,нефроны,почки...
1 - Найдите наименьшее значение функции f(x) =3-2cos3x...
3 - Постройте график функции y=4x-1. С графика укажите значение аргумента...
1 - Памагите составте диалог на тему моя семья на казахском...
1 - Қазақ әдебиетіне кластер ...
1 - - из двух поселков, расстояние между которыми 57 км, навстречу друг...
1 - РЕШИТЕ !Тест на тему «Глагол» 1.Укажите вопросы, на которые может...
3 - Распорядок дня учителя диолог как можно быстрее ...
1 - Сочинение на тему - My plans for summer vacation - на английском...
2
Объяснение:
Всі числа які кратні 6 утворюють арефметичну прогресію зі різницею d = 6; і першим членом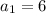 , так як найменше натуральне число яке кратне 6 це 6. Останній член прогресії
, так як найменше натуральне число яке кратне 6 це 6. Останній член прогресії 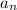 = 540.
= 540.
Знайдемо кількість членів :
540 = 6 + 6 * (n - 1);
6 + 6n - 6 = 540;
6n = 540;
n = 90.
Сума n членів арифметичної прогресії знаходиться за формулою: