1. Алгебра
  2. Знайдіть суму перших десяти членів

Знайдіть суму перших десяти членів арифметичної прогресії (аn), якщо а6 = 45, a14 = -43.

Halimali10 Halimali10    3   31.03.2020 13:25    16

Ответы
464679рли 464679рли  12.10.2020 10:20

505

Объяснение:

Формула n-го члена арифметической прогрессии: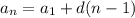 a_{n} = a_{1} + d(n - 1)

a_{6} = a_{1} + d(6 - 1) = a_{1} + 5d = 45\\\\a_{14} = a_{1} + d(14 - 1) = a_{1} + 13d = -43\\

Решим систему и найдем первый член прогрессии и разность прогрессии:

\left \{ {{ a_{1} + 5d = 45} \atop { a_{1} + 13d = -43}} \right. \\\\\left \{ {{ a_{1} = 45 - 5d} \atop { a_{1} + 13d = -43}} \right. \\\\\left \{ {{ a_{1} = 45 - 5d} \atop { 45 - 5d + 13d = -43}} \right. \\\\\left \{ {{ a_{1} = 45 - 5d} \atop { 8d = -88}} \right. \\\\\left \{ {{ a_{1} = 45 - 5*(-11)} \atop { d = -11}} \right. \\\\\left \{ {{ a_{1} = 100} \atop { d = -11}} \right.

Найдем сумму первых десяти членов прогрессии по формуле:

S_{n} = \frac{2a_{1} + d(n - 1)}{2} *n, тогда

S_{10} = \frac{2*100 + (-11)(10 - 1)}{2} *10 = (2*100 - 99)*5= 101*5 = 505

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
biolev biolev  22.12.2020 19:00
Изготовлено 90 деталей. Какова вероятность, что будет ровно 50 бракованных. Вероятность что деталь бракованная 0.35...
Mushvi Mushvi  22.12.2020 18:59
5класс математика автор с к кыдыралиев задача...
elviracernosazo elviracernosazo  22.12.2020 18:59
Укажіть функцію , графіком якої є гіпербола а)у=-2х б)у=2х^z в)ху=2 г)у=2​...
NancyKorea NancyKorea  22.12.2020 18:59
Для функции f(x)  найти первообразную, график которой проходит через точку М. f(x) = 2х +1 точка М...
Поли322 Поли322  22.12.2020 18:58
да по братски Они последние Найдите координаты точки пересечения графиков функций y = - 3x + 18 и y = 12x + 78​...
Cole21 Cole21  23.10.2020 17:22
ЧЕРЕЗ 40 МИН ЗДАВАТЬ УМОЛЯЮ...
Csgopro1 Csgopro1  23.10.2020 17:22
Указать направление ветвей пароболы,координаты твешин параболы и написать уравнение х симметрии пораболы...
Эльмаз07 Эльмаз07  23.10.2020 17:23
При якому значенні m вектори а (6; 0; 12) і b (-8; 13; m) перпендикулярні?...
Игнат282 Игнат282  23.10.2020 17:23
Математика 5 класс!Сколько единиц в числе: 1111110? 10101101? 11000011? 11010000?...
aisylu0706 aisylu0706  23.10.2020 17:23
Выпешите координаты выкторов...

Популярные вопросы