Знайдіть похідну функцію:
2) у=4х^3-2/х
3) у=3/х -2√х+7
4) у=5sin x-7 cos x​

Відповідь:

Пояснення:

2)   у=4х^3-2/х  = 4x^3 - 2x^(-1)

Використовуємо формулу похідної від степеня: (x^n)' = n * x^(n - 1) і похідної від суми: (u + v)' = u' + v'

y' = (4x^3)' - (2x^(-1))'

Виносимо константу   y' = 4(x^3)' - 2(x^(-1))'

y' = 4 * 3 * x^2 - 2 * (-1) * x^(-2) = 12x^2 + 2/(x^2)

3) у=3/х -2√х+7 = 3 * x^(-1) - 2 * x^0,5  + 7

y' = 3 * (x^(-1))' - 2 * (x^0,5)'  + 7' = 3 * (-1) * x^(-2) - 2 * 0,5 * x^(0,5 - 1) + 0 =

= -3/x^2 - x^(-0,5) = -3/x^2 + 1/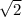

4) у=5sin x-7 cos x​

Використовуємо формули похідної від sin x i cos x:

 (sin x)' = cos x;    (cos x)' = -sin x

y' = 5 * (sin x)'  - 7 * (cos x)' = 5cos x + 7sin x