Знайдіть перший член геометричної прогресії (bn), якщо b5 = 162; q = -3.
Другие вопросы по теме Алгебра
Популярные вопросы
- На прямолинейный проводник, по которому течет ток 1,5 а, в однородном...
3 - Выбери и запиши уравнение, корнем которого является значение выражение...
1 - Решить уравнение 1)√2cos(pi/4 + x) - cosx=1 2)√2sin(pi/4 - x/2) + sin(x/2)=1...
3 - Міні твір моя майбутьня професія проводник...
1 - Решите составляй уравнения . в треугольнике один угол на 20° больше...
2 - С1994 года 22 августа в нашей стране отмечается день государственного...
3 - Укажiть безхребетних тварин, яким притаманний непрамий розвиток: а)...
2 - Ставьте глаголы во второе лицо единственного числа. 1)родину на (не)...
1 - Завтра сдавать! у меня семья из 3 человек : мама и 2 ребенка . у мамы...
3 - Описание страны нужно описать италию различные факторы : население ,...
2
ответ: 2
162=b1×(-3)^4
162=b1×81
b1=2
ответ: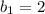 .
.
Формула общего члена геометрической прогрессии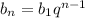 .
.