Знайдіть область допустимих значень виразу:
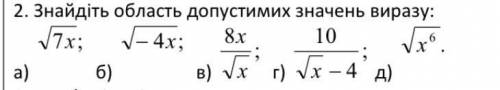
Другие вопросы по теме Алгебра
Популярные вопросы
- Чого більше молекул чи хімічних речовин?...
3 - 617.76: (38,691-34+0.309-4.56)*0.01 решите в столбик каждое действие если будет...
2 - My mother was expecting me on friday, i was arriving on thursday. a. little...
1 - Расскажите (или напишите), как вы изучали тему «типы речи». каким типом речи...
1 - Придумайте 3 или вспомните свой конфликт между прадовцом (опишите 3 конфликта...
2 - Производством каких товаров известен твой регион? (регион: гатчина)...
1 - Найти область определения функции...
1 - Что такое крестьянский труд для матрены?...
1 - Что, на ваш взгляд, изменилось, когда империя начала терпеть поражения?...
2 - Решить! 1. вынести множитель из-под знака корня: √8³ , a ≥ 0...
2
Подкоренное выражение должно быть неотрицательным. Знаменатель дроби должен быть отличен от 0 .