1. Алгебра
  2. Знайдіть найменший додатний

Знайдіть найменший додатний корінь рівняння
1-sin 2x=(sin2x+cos 2x)^2

win66123 win66123    3   09.04.2023 08:42    13

Ответы
BlackL706 BlackL706  09.04.2023 08:43

Наименьший положительный корень \dfrac{\pi }{3}.

Объяснение:

Найти наименьший положительный корень уравнения

1-sin2x=(sin2x+cos2x)^{2}

Раскроем скобки в правой части уравнения, для этого применим формулу сокращенного умножения

(a+b)^{2} =a^{2} +2ab+b^{2} .

1-sin2x=(sin2x+cos2x)^{2};\\1-sin2x=sin^{2} 2x+2sin2x\cdot cos2x+cos^{2} 2x

Так как по основному тригонометрическому тождеству

sin^{2} 2x+cos^{2} 2x=1,

то получим

1-sin2x=1+2sin2x\cdot cos2x;\\2sin2x\cdot cos2x+sin2x =0;\\sin2x( 2cos2x+1)=0;\\ \left [\begin{array}{l} sin2x = 0, \\ 2cos2x+1=0; \end{array} \right.\Leftrightarrow\left [\begin{array}{l} 2x = \pi n,~n\in\mathbb {Z}, \\ cos2x=-\dfrac{1}{2} ; \end{array} \right.\Leftrightarrow\left [\begin{array}{l} x = \dfrac{\pi n}{2} ~n\in\mathbb {Z}, \\ \\2x=\pm\dfrac{2\pi }{3}+2\pi k ,~k\in\mathbb {Z} \end{array} \right.\Leftrightarrow

\Leftrightarrow\left [\begin{array}{l} x = \dfrac{\pi n}{2} ~n\in\mathbb {Z}, \\ \\x=\pm\dfrac{\pi }{3}+\pi k ,~k\in\mathbb {Z} \end{array} .

Найдем наименьший положительный корень.

1) При  n = 1    получим положительный  корень x=\dfrac{\pi }{2}

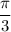2) При k=0 получим два корня  \pm\dfrac{\pi }{3}, но положительным будет \dfrac{\pi }{3}.

Наименьшим будем корень \dfrac{\pi }{3}.

#SPJ1

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
aziko2002 aziko2002  04.06.2019 17:30
1. какие из указанных чисел являются: рациональными и иррациональными? корень 36/49; корень 7; 1,6 (2); корень5 +2...
Lisa18811 Lisa18811  04.06.2019 17:30
Уравнения, сводящиеся к простейшим заменой неизвестного. 1) cos^2x+5cosx-6=0 2) 2cos^2x+5cosx+3=0 3)5tg^2x+6tgx+1=0 4)4tg^2x-7tgx-2=0 5)cos^2x-2cosx+1=0...
Nadezhda3422 Nadezhda3422  04.06.2019 17:30
Найдите приращение функции у=sin x при переходе от точки х0=0 к точке х1, если 1) х1= п/6 найдите приращение функции у=2sin x * cos x при переходе от точки х0=0 к точке х1,...
strebkov222 strebkov222  04.06.2019 17:30
Вычислите: sin15cos7-cos11cos79-sin4sin86...
спаситепомогите111 спаситепомогите111  04.06.2019 17:30
)к квадратным неравенствам общего вида следующиее неравенство (2x-1)²...
nikitaviktorov9 nikitaviktorov9  23.02.2020 18:56
Укажи рівняння прямої, зображеної на даному рисунку: y−3=0 2x=4 -6x=18 −x+4=0 x−3=0 −6y=12...
crazy660 crazy660  23.02.2020 18:55
вообщем нужно сократить дробь​...
янбаян янбаян  23.02.2020 18:55
Интеграл от 0 до 3 (1-x/3)^2dx​...
andreyffyff andreyffyff  23.02.2020 18:54
Графіки функції y = 0,5 x – 3, y = -4x + 6 і y = kx перетинаються в одній точці. Знайдіть значення k. Побудуйте в одній системі координат графіки цих функції....
yulya678 yulya678  23.02.2020 18:53
Найди периметр треугольника со сторонами 5 см 15 см и 9 см...

Популярные вопросы