Знайдіть:
1) кількість усіх двоцифрових натуральних
непарних чисел, менших від 78;
2) суму всіх двоцифрових натуральних непар-
них чисел, менше 78.

1) 34.

2) 1496

Объяснение:

1) Одне з найменших непарних двоцифрових чисел - це 11, позначимо його за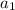 . Друге таке число буде 13, нехай воно буде 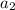. А найбільше непарне двоцифрове число (менше від 78) - це 77, нехай воно буде .

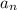2) Тоді: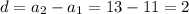 - різниця арифметичної прогресії.

3) За формулою АП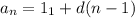 виразимо n, і це буде відповіддю на перше запитання, адже n - це кількість чисел, з яких складається АП:

4) Суму всіх двоцифрових натуральних непарних чисел (менше за 78) знайдемо із формули суми АП: