Алгебра: Значення області визначення функції 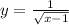А ()Б[)В(]Г.()

Значення області визначення функції $y = \frac{1}{ \sqrt{x - 1} }$
А ()
Б[)
В(]
Г.()

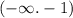
$( - \infty . - 1)$
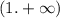
$(1. + \infty )$
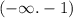
$( - \infty . - 1)$
$(1. + \infty )$

Ответы

polly132 19.11.2020 13:12

$(1;+\infty)$

Объяснение:

Область значений функции - все значения, которые может принимать функция

Функция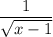 $\displaystyle \frac{1}{\sqrt{x-1}}$ может принимать следующие значения:

Корень всегда положителен или равен 0. но так как мы делим на этот корень, то нулю он равным быть не может.

Далее при любых х ОТ 1 корень существует, а значит его значение определено. Тогда область значений данной функции -

$\mathbb{E}(\displaystyle \frac{1}{\sqrt{x-1}})=(1;+\infty)$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

Evagevko 02.03.2019 14:40

(3x++6)=14 нужен ответ и проверка ! ! !...

ваня1259 02.03.2019 14:40

КристинаСтерликова 20.03.2019 15:50

Решить примеры под цифрами 2,4,6,8...

lisa301 20.03.2019 15:46

Решите уравнение √5x+8=6 √x^2-4x+13=5 √x^2-4-√8x+5=0 √2x^2-5x+1=x-1...

Bopauov26Ernar 10.09.2019 10:40

Elkhadi54Skorpion 10.09.2019 10:40

Решите уровнение а) 2х-1.8=5.3 б)7.9+5х=4.6...

alena10003 10.09.2019 10:40

senyaavdeev07 10.09.2019 10:40

proskurina773 23.12.2020 22:19

198219821982 23.12.2020 22:18