1. Алгебра
  2. Значение какого из выражений

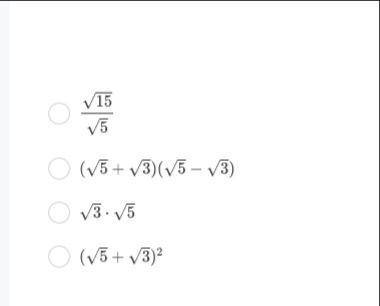
Значение какого из выражений является числом рациональным?


Значение какого из выражений является числом рациональным?

wellbiss wellbiss    2   31.05.2020 09:46    1

Ответы
wolf13131 wolf13131  15.10.2020 11:11

Смотри в решении.

Объяснение:

1) Проверяем 1 выражение:

\frac{\sqrt{15}}{\sqrt{5}} \\\sqrt{\frac{15}{5}}=\sqrt{3} \\

Следовательно, значение приведенного выше выражение является иррациональным.

2) Проверяем 2 выражение:

(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})\\5+\sqrt{5}\sqrt{3}-\sqrt{5}\sqrt{3}-3\\ 5-3=2

Следовательно, значение приведенного выше выражения является рациональным.

3) Проверяем 3 выражение:

\sqrt{3}\sqrt{5}\\\sqrt{3*5}=\sqrt{15}

Следовательно, значение приведенного выше выражение является иррациональным.

4) Проверяем 4 выражение:

(\sqrt{5}+\sqrt{3})^2 \\5+2\sqrt{5}\sqrt{3}+3\\5+2\sqrt{5*3}+3\\5+2\sqrt{15}+3\\2\sqrt{15}+8

Следовательно, значение приведенного выше выражение является иррациональным.

ПОКАЗАТЬ ОТВЕТЫ
historican historican  15.10.2020 11:11

\frac{ \sqrt{15} }{ \sqrt{5} }

\sqrt{3}

__________

( \sqrt{5} + \sqrt{3} ( \sqrt{5} - \sqrt{3} )

5 - 3

2

__________

\sqrt{3} \times \sqrt{5}

\sqrt{15}

__________

( \sqrt{5} + \sqrt{3} ) {}^{2}

5 + 2 \sqrt{15} + 3

8 + 2 \sqrt{15}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
blumkin2002 blumkin2002  31.05.2019 04:30
Установка двух счетчиков воды (холодной и горячей) стоит 3200 руб.до установки счетчиков александр платил за водоснабжение ежемесячного 1200 руб.после установки счетчиков оказалось...
Yanaaa13 Yanaaa13  31.05.2019 04:30
Решите ! 1) вычислите 2) найдите значение выражения: 3) представьте выражение в виде суммы: 4) вычислите: 5) расположите в порядке возрастания числа 6) найдите значение выражения:...
алёчек алёчек  31.05.2019 04:30
Найди площадь квадрата со стороной (√5-2)см...
dedovdima14 dedovdima14  31.05.2019 04:30
Какое из выражений тождественно раво произведению (4p-q)(5p-2q)? 1) (2q-5p) (q-4p) -4) (2q-5p) 3)(4p-q) (2q-5p) 4)(5p-2p) (q-4p)...
оаосов оаосов  31.05.2019 04:30
(две девятых -2,6)·4,5 решите , с решением))...
Felissia12 Felissia12  31.05.2019 04:30
Решить уровнение с решением! 25х: 2=х: 2+384...
ssssss22 ssssss22  19.05.2020 15:51
У выражение (4-у)(4+у)-2у(2у²-1)+4у³...
BaBaika322 BaBaika322  19.05.2020 15:51
Найдите допустимые значение переменной в выражении 3х-7/х(2х+5)...
ytxrgh ytxrgh  19.05.2020 15:51
Длина волны λ=5,6×10*-7 м..Определите энергию данного фотона(c=3*10^8 м/с, h=6,62*10^-34 Дж*с...
Ask2017 Ask2017  19.05.2020 15:51
Разложите на множители квадратный трёхчлен: 1) 2 − 5 − 24; 2) 3 2 − 10 − 8...

Популярные вопросы