Желательно с подробным решением.
Другие вопросы по теме Алгебра
Популярные вопросы
- Вольтметр с некоторым пределос измерения напряжения uпред имеет внутреннее сопротивление...
1 - Объясните,почему нельзя удерживать мочу в организме?...
3 - Начальная форма имени существительного -это...
2 - Надо расставить знаки между 3 3 3 3=4 и 3 3 3 3=8,можно скобки...
2 - Сочинение по .яз на тему моя любимая ! ! выручите кто -...
3 - Морфологический разбор глагола подскочил...
3 - Решить неполные квадратные уравнения 1) 3х²-12х=0 2) 4х²+36=0 3) 6х²-18=0 4) 25·у²-1=0...
3 - Тургенев. отцы и дети второй цикл странствий базарова (гл. 22-27) анализ эпизода...
3 - Сочинить сказку о приключении в экосистеме...
1 - Скорость некоторой реакции при 20 °с составляет 0,016 моль/(л*с), а при температуры...
3
1.![f' = \frac{1}{5} x^\frac{-4}{5} + 2*3x^2-4 = \frac{1}{5\sqrt[5]{x^4} } +6x^2-4\\f'(1) = \frac{1}{5} +6-4=\frac{11}{5}](/tpl/images/0225/7220/2bf49.png)
2.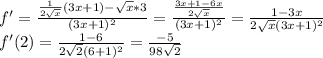
3.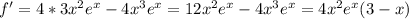
4.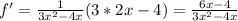
5.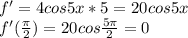
6.