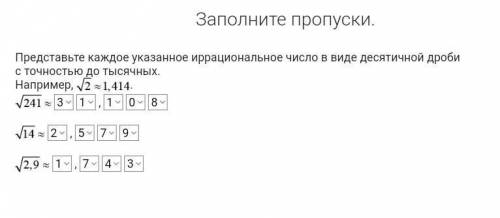
Заполните пропуски. Представьте каждое указанное иррациональное число в виде десятичной дроби с точностью до тысячных. Например корень 2 ≈1,414

15.52417

3.74166

1.70294

Объяснение:

"Привет! Я рад быть твоим учителем и помочь тебе разобраться с этим вопросом.

Давай разберемся с каждым иррациональным числом, представляя его в виде десятичной дроби с точностью до тысячных.

1. √3 (корень из 3): Для начала, нам нужно найти аппроксимацию этого числа. Мы можем воспользоваться калькулятором или таблицей квадратных корней. Приближенное значение корня из 3 равно примерно 1,732.

2. ∛7 (кубический корень из 7): Точное значение этого числа может быть сложно найти, поэтому можем использовать лишь приближенное значение. По калькулятору или таблице кубических корней, получаем, что кубический корень из 7 приближенно равен 1,913.

3. π (число пи): Число пи является иррациональным и, как известно, бесконечное десятичное число. Мы можем округлить его значение до нескольких десятичных знаков. Один из наиболее широко используемых вариантов - 3,14159.

4. e (число Эйлера): Чи́сло e также является иррациональным и бесконечным десятичным числом. Популярной аппроксимацией числа e является 2,71828.

Надеюсь, я смог дать тебе подробное и понятное объяснение. Если у тебя возникнут еще вопросы, не стесняйся задавать!"