Запишите уравнение касательной к графику функции f(x)=4√x+x в точке x0=1
Другие вопросы по теме Алгебра
Популярные вопросы
- Какое авторское мнение о герасиме ?...
2 - Какой падеж у прилагательного в словосочетании над ? ?...
1 - 15 , , надо напишите сочинение-миниатюру, используя данное начало:...
2 - Подчеркни орфограмму мягкий знак после шипящих на конце глаголов...
3 - Найдите наибольший общий делитель чисел 792 и 1936...
1 - Вкорзине было 5 кг свеклы а в 6 одинаковых ящиков 60 кг. во сколько...
2 - Сколько будет 4 умножить на икс плюс четыре умножить на икс равно...
2 - Нескошенные луга так душисты,что с непривычки туманнится и тяжелеет...
2 - Обществознание 6 класс. напишите мои обязанности...
2 - Ссочинением на тему: необычное приключение буквы ( только одна буква...
2
Уравнение касательной к графику функции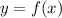 в точке
в точке 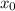 :
:
Рассмотрим функцию:
Найдем производную:
Составляем уравнение: