записать уравнение прямой, проходящей через точку a(3, 1) перпендикулярно к прямой bc, если b(2, 5), c(1, 0)
Другие вопросы по теме Алгебра
Популярные вопросы
- Ғұлама Әл Фарабидің қасиетін ашатындай 5сын есім жазыңыз...
2 - в равнобокой трапеции один из углов равен 120 градусов диагональ трапеции...
1 - Расположи данные слагаемые в порядке возрастания и найди значение выражения:-14;...
1 - Это Существует мнение, что «устойчивое развитие сельского хозяйстваразвитие,...
1 - Олимпиада по специальности Экономика и бухгалтерский учет Тема: Ценные бумаги...
1 - Речевые ошибки т от 40 С объяснениями, если возможно >...
3 - Найдите словосочетание со связью примыкание * пышущий здоровьем чайник закипел...
3 - Три економісти заповнюють документи і складають у спільну папку, причому...
3 - Обществе служит для достижения общих целийи удовлетворения общественных потребностей...
2 - ребята, кто вяжет, что мне делать? нитка в середине, как вернуть на место?...
3
(x-x1)/Аx=(y-y1)/Аy
Координаты вектора ВС (х2-х1; у2-у1)
ВС (1-2;0-5)
ВС (-1; -5)
Координаты вектора перпендикулярного ВС (5; -1)
Тогда уравнение прямой выглядит
(х-3)/5=(у-1)/-1
х-3=-5у+5
5у=8-х
у=(8-х)/5
х+5у-8=0
Пошаговое объяснение:
Найдем вектор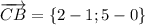
Заметим, что уравнение прямой имеет вид А₁х+В₁у+С₁=0.
Известно, что вектор {A₁; B₁} - перпендикулярен данной прямой, поэтому вместо А₁ и В₁ подставим координаты вектора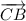 .
.
Получается х+5у+С₁=0. Найдем С₁ с подстановки в последнее уравнение координат точки A(3, 1).
3+5*1+С₁=0
8+С₁=0
С₁=-8.
В итоге уравнение искомой прямой принимает вид х+5у-8=0.