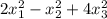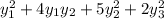Закон инерции квадратичной формы. Может ли форма в одном базисе иметь вид $2x^{2}_{1} -x^{2}_{2} +4x^{2}_{3}$ , а в другом $y^{2}_{1}+4y_{1}y_{2}+5y^{2}_{2}+2y^{2}_{3}$ ?

Ответы

dia207 22.07.2021 22:10

Закон инерции квадратичной формы гласит, говоря неформальным языком, что количество положительных коэффициентов, как и количество отрицательных коэффициентов не зависит от базиса, лишь бы квадратичная форма в таком базисе не имела слагаемых в виде произведения двух координат (иными словами, чтобы были только квадраты ). В первом случае форма имеет канонический вид (так мы говорим, когда нет произведения типа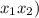 x_1x_2) . Подсчитываем: положительных коэффициентов два, отрицательный один (есть даже такой термин - положительный индекс инерции 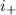i_+ , отрицательный индекс инерции 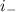i_- ; у нас 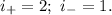$i_+=2;\ i_-=1.$ Во втором случае вид неканонический, но мы можем легко получить канонический, сделав так:

y_1^2+4y_1y_2+5y_2^2+2y_3^2=(y_1+2y_2)^2+y_2^2+2y_3^2 .

Заменять на новые буковки не будем, поскольку три квадрата видно и так. Поэтому в этом случае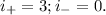 i_+=3; i_-=0. Мы видим другой набор из положительного и отрицательного индексов инерции, поэтому ответ в задаче: не может