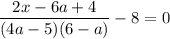Задано уравнение 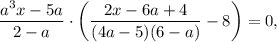 где
где  — переменная,
— переменная,  — постоянная. 1. При каких значениях
— постоянная. 1. При каких значениях  уравнение не имеет решений?
уравнение не имеет решений?
2. При каком значении  уравнение имеет множество решений?
уравнение имеет множество решений?
3. Решите данное уравнение в зависимости от значений  .
.
Другие вопросы по теме Алгебра
Популярные вопросы
- Можно ли считать ум богатством человека.почему? (сочинение) ...
3 - Определи стороны многоугольника р вычесли ихпериметры...
1 - Впервого поля вывезли 16 стогов сена, а со второго на 8 стогов...
1 - Расставь скобки так, чтобы равенства были верными.9-4+2=3,9-4+2=7,...
1 - Решите . за 5часов турист км.сколько он за 7 часов,двигаясь с...
2 - Придумайте стих про клетку на 5 строк...
2 - Составить предложения в которых в качестве обращения использовались...
3 - Заполните таблицу противоположные числа н: р а и -а 6 класс номер...
2 - Как будет начальная форма местоимения с предлогом над вами...
1 - Какие причина влияют на размещение людей?...
2
1. Если хотя бы один из знаменателей дробей будет равен нулю, то уравнение не будет иметь смысла.
Таким образом, если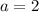 или
или 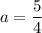 , или
, или 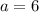 , то уравнение не имеет решений.
, то уравнение не имеет решений.
2. Произведение множителей равно нулю тогда, когда хотя бы один из них равен нулю.
Решим первое уравнение совокупности.
Если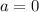 , то имеем уравнение
, то имеем уравнение 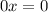 , решением которого является любое число.
, решением которого является любое число.
3. Если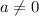 , то
, то 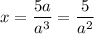
Решим уравнение