Задано функцію f(x)=x-1/x . 1. Побудуйте графік функції y=f(x). 2. Знайдіть похідну функції f(x) . 3. Запишіть рівняння дотичних до графіка функції y=f(x), які паралельні прямій y=x4 . 4. Знайдіть найменше значення функції x−f(x) на проміжку [1/2;∞) .

Другие вопросы по теме Алгебра
Популярные вопросы
- 1) cos(3x/4)=0 2) sinx -1/2 3) ctgx или = 1...
2 - Какие события повлияли. на развитие страны великобритания...
1 - Выберите для каждого значения наиболее подходящий тип данных из таблиц...
3 - Переведите с на казахский! нужно жили когда-то в степях сарыарки несколько...
3 - Даты известных людей (завтра уже урок)...
3 - Напишите два изменения которые затронули музыкальное исскуство ( кратко)...
2 - Найдите наибольший общий делитель 46 и 69...
1 - Имя князя киевского из былины 8 букв...
1 - Вкаких случаях в языке в окончании глагола не пишется окончание s ?...
3 - Написать показательную форму z20 z=3+корень из 3i...
1
Все в объяснениях.
Объяснение:
1. Постройте график функции y=f(x).
Гипербола, полученная сдвигом графика у=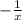 на 1 вверх по оу. у(-2)=0,5 ;у(-1)=1 ;у(-2)=0,5 ;у(2)=-0,5 ;у(1)=-1 ;у(2)=-0,5
на 1 вверх по оу. у(-2)=0,5 ;у(-1)=1 ;у(-2)=0,5 ;у(2)=-0,5 ;у(1)=-1 ;у(2)=-0,5
2. f '(x)= ( ) ' =
) ' =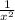 .
.
3. Уравнения касательной y =к (x −x₀)+f (x₀) .
Прямая y=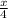 , к=1\4.
, к=1\4.
Найдем точку касания
(x-2)²=0 , x=2.
f (2)=-1\2+1=0,5
y =0,25* (x −2)+0,5
у=0,25х
Вторая касательная пройдет через х=-2
f (-2)=1\2+1=1,5
y =0,25* (x −2)+1,5
у=0,25х+1
4. Наименьшее значение функции у'=(x−f(x) ) '=(х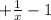 )' =
)' =
=1 -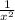 =
=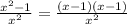 .
.
у'=0 ,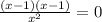 ,х=1 , х=-1.
,х=1 , х=-1.
На промежутке [1/2;∞) лежит только х=1
у'______[1\2] - - - - -(1)+ + + + +
y ↓ ↑
x=1 точка минимума.
Наименьшее значение может быть при х=1\2 или х=1:
у(1\2) =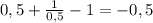 .
.
у(1)= 1+1-1=1.
Наименьшее значение функции х-f(x) равно -0,5