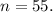задания последовательности с формулы n-го члена, называется: *
Табличный
Словесный
Рекуррентный
Аналитический
2.Последовательность Фибоначчи это задания числовой последовательности. (вставьте пропущенное слово) *
табличный
аналитический
словесный
рекуррентный
3.Найдите закономерность и продолжите последовательность чисел 6,7; 6,2; 5,7; 5,2; ... . *
4.Запишите 6 первых членов последовательности натуральных чисел кратных 3-м. Укажите, где записаны первый, четвертый и одиннадцатый члены последовательности. *
1; 4; 11
3; 12; 33
3; 6; 66
1; 9; 30
5. Последовательность (Yn) задана аналитически. Запишите четвёртый член последовательности Yn=2 в степени n
16
2
32
8
6.Последовательность (An) задана аналитически. Найдите 3 первых члена этой последовательности An=4*n-9
5; 1; -3
-5; -1; 3
0; -5; -1
-1; 3; 7
7.Выберете формулу n-го члена последовательности, первыми членами которой являются числа 2; -1; -4; -7; ... .
5-3n
-3n
2-3n
-3+2n
8. Последовательность (Dn) задано формулой n-го члена Dn=2*n*n-5. Является ли число 5 члнном этой последовательности?
Да
Нет
9. Последовательность (Xn) задана формулой n-го члена Xn=50 - 3*n. Сколько положительных членов содержит данная последовательность?
10. Найдите номер члена последовательности (Bn), заданной формулой Bn=0,125*(n-15)*(n-15), равного 200
Другие вопросы по теме Алгебра
Популярные вопросы
- Укажіть дріб, у якому 3 десятки 2 сотих: а) 30,02; б) 230; в) 30,2; г)...
3 - Знайти 5 член і суму 4 перших членів ї прогресії(bn) якщо b1=27,q=1/3...
1 - Найдите объём параллепипед a=4 см, b= 3 см, c= 5 см....
2 - Отношение тома сойера и гека финна к учебе. если можно то с доказательством...
2 - Римме подарили 110 тетрадей. и в 20 раз больше дали ей в школе.сколько...
2 - Из данных величин составить два верных неравенства 1ч20мин. 12дм. 1ц 20...
2 - Речення з підметом , присудоком, додаток, означення, обставиною. желательно...
2 - Сколько столетий назад закончилась эпоха средних веков...
1 - Синтаксичиский разбор предложения машины автобусы траллейбксы трамваи...
2 - 380.007*(100.100-99.999)+100.003*3=?...
1
1) Аналитический.
2) Рекуррентній.
3) Это арифметическая прогрессия с разностью –5. Продолжается так: 6,7; 6,2; 5,7; 5,2; 4,7; 4,2; 3,7; 3,2 ...
4) Первое число кратное трём, это тройка. Поэтому подходят либо второй, либо третий вариант. Четвёртый член должен быть равен 3*4=12, поэтоу правильный ответ — второй: 3; 12; 33.
5)
6)
7) Это арифметическая прогрессия.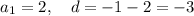
8)
ответ: нет, не является, потому что должно быть натуральным числом.
должно быть натуральным числом.
9)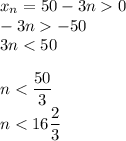
Наибольшее натуральное , удовлетворяющее этому неравенству, — это 16.
, удовлетворяющее этому неравенству, — это 16.
ответ: 16 членов.
10)
Второе решение не подходит, поскольку должно быть натуральным числом.
должно быть натуральным числом.
ответ: