Задание номер 4 Найти производную функции
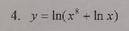
Другие вопросы по теме Алгебра
Популярные вопросы
- Решить уравнения 1) (х-4)(х+-5)(х-6)=3х 2) 12х в квадрате -(3х-4)(4х+1)=19...
2 - Как образуются ледники? коротко 9...
1 - Количество ног один из признаков в систематике...
1 - C++ вывести на экран все нечетные числа от 1 до 20, через цикл for....
3 - Существуют ли радиоактивные ядра атомов?...
1 - Рассчитать массу оксида меди(2),полученного при сжигании 3,2 меди...
3 - Постройте график функции а)у=-3х; б)у=2х-1 является ли функция возрастающей...
2 - Нужен перевод летом я плаваю осенью я иду в школу зимой я катаюсь...
2 - Главная мысль рассказа ю и коваль -вот шагает гражданин...
1 - Втрех пакетах был творог .когда из первого пакета взяли 1\4 кг. из...
2
производная сложной функции, внешняя - логарифмическая, зависит от суммы степенной и логарифмической. Поэтому схема нахождения производной функции у=㏑v, найти производную логарифма и умножить на производную v=x⁸+㏑x, т.к.
у'=(1/v)*v'
у'=1/(x⁸+㏑x)*(x⁸+㏑x)'=(8х⁷+(1/х))/(x⁸+㏑x);
Не четко виден знак. если в скобках минус,ТО ОТВЕТ ТАКОЙ
у'=(1/v)*v'
у'=1/(x⁸-㏑x)*(x⁸-㏑x)'=(8х⁷-(1/х))/(x⁸-㏑x);