Задание на фотографии прикрепленной
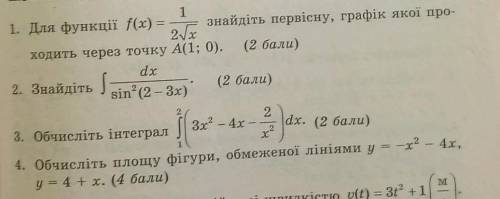
Другие вопросы по теме Алгебра
Популярные вопросы
- Падежи в словах поля города океаны поезда...
2 - Почему образование должно быть бесплатным? 10-15 предложений...
1 - Социальные институты называют фабриками воспроизводство общественныхотношений...
3 - Основной оксид + металл кислотный оксид + металл амфотерный оксид + металл...
1 - Запиши тексты загадок и отгадки. какие части речи использованы в них? 1,не...
1 - Из обувных фабрик москвы даёт за 3 минуты 75 пар обуви.сколько пар обуви...
3 - Решите уравнение: (дробь) 5х^2-х /х=0...
2 - Почему автор закончил роман смертью главного героя отцы и дети ? , надо....
3 - Чем мотивировано великодушное отношение отца земфиры и других цыган к убийце...
1 - Финикия - слово произошедшее от греческого фойны или египетского фенеху...
1
1.
A(1;0)
Первообразная, проходящая через точку A
2.
3.
4.