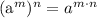Задание №3 Выполнить умножение многочленов с формулы разности квадратов 1. (х – 13)(х+13)
2. (11 +5у)(11-5у)
3. (12с – 5у)(12с+5у)
4. (9с2+2)(9с2 -2)
5. (10р – 7у)(10р+7у)
6. (1 – х5)(1+х5)
7. (р4 +6с)(р4-6с)
8. (20р4 + 7у2)(20р4 – 7у2)
9. (а -2с)(а+2с)
10. (х3 – 6с4)(х3+6с4)
Другие вопросы по теме Алгебра
Популярные вопросы
- Масса гуся 4 5/12 кг, а масса страуса в 7 раз больше. на сколько кг...
2 - Какие отношения относятся преимущественно к сфере жизни общества?...
1 - Напиши слова с данными суффиксами ист, ник , чик . слова связь, летать,...
3 - Полажительное заряженные ионы в растворе называют...
1 - Три уравнения реакций, характеризующих свойства оснований....
2 - Вычислите молекулярные массы следующих веществ оксида магния- mgo; соды...
3 - Сделать синквейн о колокольчиках. из сказки город в табакерке....
1 - Сочинения про лондон 7 предложений ....
1 - Что значит личное окончания глаголов...
3 - Как решить уравнение 70902+? *2--95000...
1
Объяснение:
Для решения используем формулу разности квадратов двух чисел:
Вспомним:
• При возведении степени в степень основание оставляют тем же, а показатели перемножают: