Задание 2 ( ).
Определите количество решений системы графическим методом:
Skrinshot 13-10-2021 170834.pngЗапишите алгоритм построения заданных графиков и подпишите их при построении.
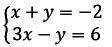
Другие вопросы по теме Алгебра
Популярные вопросы
- Номер 1345 6 класс 2 часть учебника ....
3 - 1.предлог- а) самостоятельная часть речи б) особая часть речи в)служебная...
1 - 22. Сравните Великобританию и Индию. ПоказателиДля сравненияВеликобританияИндияГеографическоеIіоложениеПлощадь,...
3 - G(x)=|x−15|+2 та f(x)=(x+2)2+6. Обчисли g(x)+f(x), якщо g(−33);f(1)....
2 - Сравните Давань и Кингха.please ...
3 - Где можно скачать « чертіщева фізика 7 клас зошит для поточного та...
3 - Сколько грамм воды получится, если разложили при нагревании 23,4 г...
3 - Лисица 1) (-3:0).(-2: 1), (3; 1). (3:2).(5:5). (5:3). (6:2),(7:2),...
3 - основи прямокутної трапеції дорівнюють 3 і 5 см знайдіть площу прямокутної...
1 - Міні твір на тему: Значення та особливости технологій хімічного виробництва...
1
Для определения количества решений системы уравнений графическим методом, нам нужно построить графики данных уравнений и исследовать их взаимное расположение.
Заданная система уравнений:
1) 2x - y = 4
2) y = 3x - 2
Давайте начнем с первого уравнения. Для построения его графика, мы можем использовать следующий алгоритм:
Шаг 1: Запишем уравнение в общем виде: y = 2x - 4.
Шаг 2: Выберем несколько значений для x (например, x = -2, 0, 2) и найдем соответствующие значения для y, используя уравнение.
Шаг 3: Построим точки (x, y) для каждой пары значений на координатной плоскости.
Шаг 4: Соединим полученные точки с помощью линии.
Шаг 5: Подпишем эту линию как график первого уравнения.
Теперь перейдем ко второму уравнению. Алгоритм для его построения будет следующим:
Шаг 1: Запишем уравнение в общем виде: y = 3x - 2.
Шаг 2: Выберем несколько значений для x (например, x = -2, 0, 2) и найдем соответствующие значения для y, используя уравнение.
Шаг 3: Построим точки (x, y) для каждой пары значений на координатной плоскости.
Шаг 4: Соединим полученные точки с помощью линии.
Шаг 5: Подпишем эту линию как график второго уравнения.
Теперь, когда у нас есть графики обоих уравнений, мы можем рассмотреть их взаимное расположение.
Найдем точку пересечения графиков, если такая есть. Для этого нужно найти значение x, при котором уравнения равны друг другу:
2x - 4 = 3x - 2.
Перенесем все переменные на одну сторону:
2x - 3x = -2 + 4,
-x = 2.
Теперь найдем значение x:
x = -2.
Подставляя значение x обратно в одно из уравнений, мы найдем соответствующее значение y:
y = 3*(-2) - 2 = -6 - 2 = -8.
Итак, мы получили координаты точки пересечения графиков: (-2, -8).
Теперь определим количество решений системы уравнений, исходя из их графического пересечения:
Если графики пересекаются в одной точке, то есть только одно решение системы уравнений.
Если графики совпадают (полностью совпадают), то у системы уравнений бесконечно много решений.
Если графики не пересекаются, то система уравнений не имеет решений.
В нашем случае, графики пересекаются в одной точке (-2, -8), следовательно, у системы уравнений есть только одно решение.
Надеюсь, это объяснение помогло вам понять решение задачи. Если у вас есть еще вопросы, не стесняйтесь задавать!