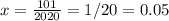Задача с параметром высокого уровня

Другие вопросы по теме Алгебра
Популярные вопросы
- 1/8+1/10= (несократимую дробь пожпалуйста очень надо...
2 - Сообщение на тему любой мужественные поступок...
2 - Що відбулося згодом в домі Хельмерів...
3 - Есе на тему один день мого життя я серед друзів...
2 - ОЧЕНЬ Великому господину, преосвященному Симеону, архиепископу...
3 - Номер очень надо + номер 7 6 класс страница ,168 номер 7,8...
3 - Що спільного у віршах ,,Чайка на крижині‘‘ і ,,Крила‘‘???...
1 - Визначи розряд числівника за будовою.сто-кількасот -...
3 - При каком значении переменной x значит выражение 2x-4=2...
2 - Нужно составить две задачи по оптике с решением и рисунком. Буду...
2
Элементарный факт: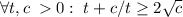
Поэтому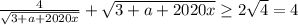 ,
,  .
.
Значит, левая часть не меньше 10. С другой стороны, она равна 10. Стало быть, все неравенства обращаются в равенства. Справедлива система: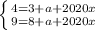 , откуда
, откуда 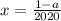 . Наибольшее решение при
. Наибольшее решение при 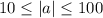 достигается при
достигается при  . Тогда
. Тогда