я больше не могу МОЛЮ ИНАЧЕ МЕНЯ УБЬЮТ с может ваш отличник сможет решить? Все таки потратил(

Ответы

NastyaLus 14.10.2020 13:30

1. Разложим, выделив полные квадраты где возможно и посмотрим, можно ли

$1) \ 4x^2-4xy+2y^2-2y+1=(2x)^2-2\cdot 2x\cdot y+y^2+y^2-2y+1 = \\ =(2x-y)^2+(y-1)^2$

Вот и получили сумму квадратов, а квадрат любого действительного числа (именно такие мы рассматриваем) неотрицателен, то данное выражение отрицательные значения принимать не может. ответ: нет.

$2) \ 1-8ab+4a^2b^2+4a^2+b^2 = (2a)^2-2\cdot 2a\cdot b+b^2 -4ab+4a^2b^2+1 = \\=(2a+b)^2+(2ab)^2-2\cdot2ab\cdot1+1^2 = (2a+b)^2+(2ab-1)^2$

Здесь ситуация аналогичная и ответ: нет.

2. Решаем уравнения

$1)\ y^3-24y^2=216-9y;\ y^2(y-24)-9(24-y)=0; \\ (y-24)(y^2+9)=0 \Rightarrow y=24$

Вторая скобка содержит в себе квадрат и положительное слагаемое, она всегда положительна, так что нулю может быть равна только первая скобка, откуда искомый корень и нашли. ответ: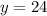 y=24

$2) \ 16x^3+12x^2=4x+3; \ 4x^2(4x+3)-(4x+3)=0; \\ (4x+3)(4x^2-1)=0; \ (4x+3)(2x-1)(2x+1)=0$

Произведение равно нулю, когда хотя бы один из сомножителей равен 0, это совокупность на языке множеств.

$\displaystyle (4x+3)(2x+1)(2x-1)=0 \Leftrightarrow \left[\begin{array}{ccc}4x+3=0\\2x+1=0\\2x-1=0\end{array} \Rightarrow \left[\begin{array}{ccc}x=-\frac{3}{4} \\x=-\frac{1}{2} \\x=\frac{1}{2} \end{array}$

В порядке убывания ответ будет такой:

$\displaystyle \frac{1}{2}; \ -\frac{1}{2}; \ -\frac{3}{4}$

3. Просто раскладываем:

$1) \4a^2-4b^2-a-b=4(a^2-b^2)-(a+b)=4(a-b)(a+b)-(a+b)= \\ =(a+b)(4(a-b)-1)=(a+b)(4a-4b-1) \\ 2) \ 9x^2-9y^2-3x+3y = 9(x^2-y^2)-3(x-y)=\\ =9(x-y)(x+y)-3(x-y)=3(x-y)(3(x+y)-1) = \\ =3(x-y)(3x+3y-1) \\ 3) 16p^2-y^2+8y-16 = (4p)^2 -(y^2-2\cdot y\cdot 4+4^2) = \\= (4p)^2-(y-4)^2 =(4p-(y-4))(4p+(y-4)) =\\ = (4p-y+4)(4p+y-4) \\ 4) \ 0.25a^2-a-b^2+1 = (0.5a)^2-2\cdot 0.5a\cdot1+1^2-b^2 = \\= (0.5a-1)^2-b^2 = (0.5a-1-b)(0.5a-1+b)$

4. Аналогично (если вы не проходили, корни, что вероятнее всего, так как это 7-ой класс, то в 1 примере последнее на пиши, остановись на предпоследнем шаге):

$1) \ a^3-7a^2-3a+21 = a^2(a-7)-3(a-7) = (a-7)(a^2-3) = \\ =(a-7)(a-\sqrt{3})(a+\sqrt{3}) \\ 2)\ 3x^4-8x^3+12x-32 = x^3(3x-8)+4(3x-8)=(3x-8)(x^3+4)\\ 3) \ a^5-6a^4+a^3-6a^2 = a^4(a-6)-a^2(a-6)=(a-6)(a^4-a^2) = \\ =(a-6)a^2(a^2-1)=a^2(a-6)(a-1)(a+1) \\ 4) \ 11x^7-11x^6+6x^5-6x^4 = 11x^6(x-1)+6x^4(x-1) =\\= (x-1)(11x^6+6x^4)=x^4(x-1)(11x^2+6)$

5. Тут уже даже первое действие дано

$1) \ 6b^2-6a^2-7b+7a=(6b^2-6a^2)-(7b-7a)=\\=6(b^2-a^2)-7(b+a) = 6(b-a)(b+a)-7(b+a)= \\ =(b+a)(6(b-a)-7)=(a+b)(6b-6a-7) \\ 2) x^4+x^3y-3x-3y = (x^4+x^3y)-(3x+3y) =\\= x^3(x+y)-3(x+y)=(x+y)(x^3-3)$