Алгебра: Y=x^3+x^2-x наименьшее значение на (-2;2)

Y=x^3+x^2-x наименьшее значение на (-2;2)

Ответы

dannovchern 15.10.2020 15:15

$y=x^3+x^2-x\ \ ,\ \ x\in (-2;2\, )\\\\y'=3x^2+2x-1=0\ \ ,\ \ x_1=-1\ ,\ x_2=\dfrac{1}{3}\\\\znaki\ y':\ \ \ \ (-2\, )+++(-1)---\Big(\dfrac{1}{3}\Big )+++(\, 2\, )\\\\x_{max}=-1\ \ ,\ \ x_{min}=\dfrac{1}{3}\\\\\lim\limits _{x\to -2+0}(x^3+x^2-x)=-2\\\\y(-1)=-1+1+1=1\\\\y\Big(\dfrac{1}{3}\Big)=\dfrac{1}{27}+\dfrac{1}{9}-\dfrac{1}{3}=-\dfrac{5}{27}\\\\\lim\limits _{x\to 2-0}(x^3+x^2-x)=10$

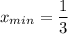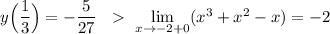Так как значение функции в точке минимума на интервале (-2;2) больше, чем правосторонний предел функции в точке х= -2, $x_{min}=\dfrac{1}{3}$ и $y\Big(\dfrac{1}{3}\Big)=-\dfrac{5}{27}\ \ \ \lim\limits _{x\to -2+0}(x^3+x^2-x)=-2$ , точка х= -2 не входит в исследуемый промежуток , то наименьшего значения функции найти нельзя. Значения функции ограничены снизу величиной (-2) .

Кстати, нельзя в этом случае найти и наибольшего значения функции на интервале (-2;2), так как

$x_{max}=-1\ ,\ \ y(-1)=1\$ . Значения функции ограничены сверху величиной 10 .

Смотри график.

Если по условию надо найти наименьшее значение функции на сегменте [-2;2 ] , то решение написано ниже.

$y=x^3+x^2-x\ \ ,\ \ x\in [-2;2\ ]\\\\y'=3x^2+2x-1=0\ \ ,\ \ x_1=-1\ ,\ x_2=\dfrac{1}{3}\\\\znaki\ y':\ \ \ \ [-2\, ]+++(-1)---\Big(\dfrac{1}{3}\Big )+++[\, 2\, ]\\\\y(-2)=-8+4+2=-2\\\\y(-1)=-1+1+1=1\\\\y\Big(\dfrac{1}{3}\Big)=\dfrac{1}{27}+\dfrac{1}{9}-\dfrac{1}{3}=-\dfrac{5}{27}\\\\y(2)=8+4-2=10\\\\y(naimen)=min\, y(x)_{[-2;2]}=-2=y(-2)$