:y(2 степень)+x(2 степень)-2xy xz-yz+ty-xt
Другие вопросы по теме Алгебра
Популярные вопросы
- Рассказ по пословицу а вы друзья как не садитесь всё в музыканты не годитесь...
1 - ІІІ тоқСАН БОЙЫНША жиынтық БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР «VT- х горарим...
3 - Чотири білки з їли 1999 горіхів, кожна не менше, ніж 100 Перша білка з їла...
3 - Визначте протяжність України від м. Чоп до с. Рання Зоря на політичній карті...
1 - Визначте географічну широту місцевості, де у дні весняного рівнодення кут...
3 - Синтаксичний розбір речення: В одну мить розсунувся протір і стали ближчіми...
3 - Почему бояре не хотели что бы Феврония была женой Петра...
2 - Решите задачку, решение не важно, нужен лишь ответ...
2 - Точки (1,0), (1,1), (2,4), (1,3), (0,5), (0,2) на координатной плоскости...
3 - найдите 6 нерегулярные формы множественного числа-books,feet,brushees,ladies,toys,knives,mice,lamps,cameras,classes,children...
3
\frac{y^2+x^2-2xy}{xz-yz+ty-xt}=\frac{(x-y)^2}{(xz-yz)+(ty-xt)}=\frac{(x-y)^2}{z(x-y)+t(y-x)}=\frac{(x-y)^2}{(z+t)(x-y)}=\frac{(x-y)}{(z+t)}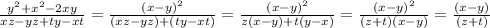
(x-y)^2=(y-x)^2