Xи y принадлежат целым числам, решите уравнение: x^2+xy+у=10x

Ответы

anutka2018 14.08.2020 16:22

$(y,x)\in\{(24,-2),(24,-12),(0,10),(0,0)\}$

Объяснение:

Если x = 0, то y = 0. Поищем другие решения, в которых x отлично от нуля.

$x^2+xy+y=10x\\y=10x-xy-x^2=x(10-y-x)$

Из последней строчки следует, что y делится на x. Подставим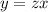 y=zx :

$zx=x(10-zx-x)\\z=10-zx-x\\zx+z+x+1=11\\(z+1)(x+1)=11$

Все возможные разложения числа 11 на два целых множителя:

$11=(-11)\cdot(-1)=(-1)\cdot(-11)=1\cdot11=11\cdot1$

Значит,

$(z,x)\in\{(-12,-2),(-2,-12),(0,10),(10,0)\}$

Вспоминая, что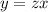 y=zx , получаем ответ.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

IndiAkent 04.02.2022 15:56

Afon7 04.02.2022 15:59

Відомо, що х+у=5, ху=-2. Знайдіть значення виразу (х-у)2...

чинка2 04.02.2022 16:00

номер 297 только третий нужен только третий...

СнежаночкаФил 04.02.2022 16:01

этояученик 04.02.2022 16:01

Pump2000 08.10.2019 18:50

Определите пересечкние промежутков [-2; 1] и (-∞; 0]...

manokhaangel 08.10.2019 18:50

SupercellTV 08.10.2019 18:50

ainexl 08.10.2019 18:50

Для функции f(x)=x-2/x+3 найдите f(x) и f(-2)....

ninadyukovap0a6fu 08.10.2019 18:50

Для функции f(x)=x+3/x-2 найдите f(x) и f(1)....