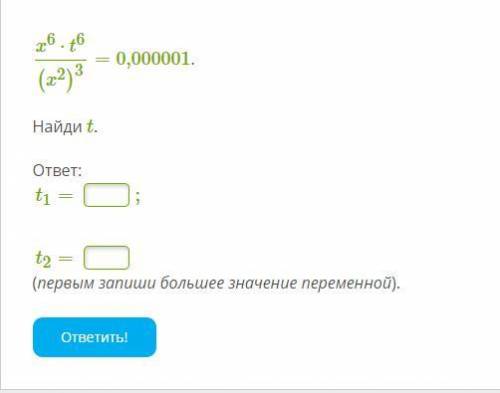
X6⋅t6(x2)3=0,000001. Найди t.

ответ:
t1=
;t2=
(первым запиши большее значение переменной).

Для решения данного уравнения, мы должны сначала избавиться от степеней и решить получившуюся квадратную уравнение.

У нас есть уравнение:
X6⋅t6(x2)3=0,000001

Для облегчения вычислений, давайте перепишем уравнение в виде:
(X⋅t)^6(x^2)^3=0,000001

Раскроем степени:
(X^6)(t^6)(x^6)(x^6)(x^6)=0,000001

Теперь объединим все основания в одно:
(X^6⋅t^6⋅x^6⋅x^6⋅x^6)=0,000001

Чтобы найти t, мы должны избавиться от всех остальных переменных, оставив только t.

(x^6⋅x^6⋅x^6)=0,000001/(X^6)=t^6

Теперь возведем обе стороны в степень 1/6:
(x^6⋅x^6⋅x^6)^(1/6)=(0,000001/(X^6))^(1/6)=t

Таким образом, мы получили значение t, равное корню 6-ой степени от (0,000001/(X^6)).

Одновременно найдем значения t1 и t2. Чтобы это сделать, представим корень 6-ой степени как два различных числа, возводя (0,000001/(X^6)) в степени 1/6 и -1/6.

t1 = (0,000001/(X^6))^(1/6)
t2 = (0,000001/(X^6))^(-1/6)

Первым запишем большее значение переменной:
t1 > t2

Но для окончательного ответа нам нужно знать значение X. Если X неизвестно, мы не сможем точно посчитать t. Так что без значения X мы не можем дать конкретного числового значения t.