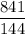X+ √x+7 + 2√x²+7x = 35-2x
(если не понятно - 4) номер в прикреплённой фотографии)
Другие вопросы по теме Алгебра
Популярные вопросы
- Хто з вчених досліджував форму Землі?...
2 - KOH+H2SO4 = K2SO4+H2O уровнять...
1 - В первой урне 4 красных и 8 синих шара. Из нее наугад вынимают три шара и перекладывают...
1 - Социальная структура в начале ХХ веке в ГА?...
2 - Прочитай выражение и найди его значение. В данном числовом выражении 4,7÷(−2) записано частное...
3 - быстрее1121113# -8+8;7-8;7;8;8;8...
2 - 3 Ознакомьтесь с общей структурой автобиографии. Опираясь на неё, составь- те свою...
1 - с алгеброй Формулы сокращённого умножения >...
2 - Структура художественого произведения 6 класс...
3 - Какие находки эпохи камня были обнаружены археологами на территории Казахстана?...
2
Проверкой убеждаемся, что ответ подходит.
В левой части уравнения можно разложить на множители выражение
Произведение равно нулю в том случае, когда один из множителей обращается к нулю
Это уравнение решений не имеет, поскольку левая часть уравнения на области допустимых значений принимает положительные значения.
Возводим обе части уравнения до квадрата.
При условии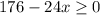 возводим обе части уравнения в квадрат
возводим обе части уравнения в квадрат
корень x = 9 не удовлетворяет условию 176 - 24x ≥ 0.
ответ: