Алгебра: X²-92=y²+2y Найдите количество пар целых чисел

X²-92=y²+2y Найдите количество пар целых чисел

Ответы

ленура21 31.01.2022 06:00

x^2-92=y^2+2y

Заметим, что если в правой части добавить 1, то получим формулу квадрата суммы. Тогда, добавим 1 и в левой и в правой части:

x^2-92+1=y^2+2y+1

x^2-91=(y+1)^2

x^2-(y+1)^2=91

Применим формулу разности квадратов:

(x-y-1)(x+y+1)=91

Заметим, что если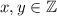 $x,y\in\mathbb{Z}$ , то обе скобки, записанные в левой части, дают целые числа.

Разложим число 91 на простые множители:

$91=7\cdot13$

Тогда, число 91 можно получить путем умножения либо чисел 7 и 13, либо чисел 1 и 91. Нужно учесть, что эти числа могут умножаться в разных порядках, а также то, что оба множителя могут поменять знак на противоположный.

Таким образом есть 8 упорядоченных пар целых чисел, в произведении дающих 91:

$(1;\ 91);\ (7;\ 13);\ (13;\ 7);\ (91;\ 1);\\ (-1;\ -91);\ (-7;\ -13);\ (-13;\ -7);\ (-91;\ -1)$

Но данные пары целых чисел соответствуют скобкам в произведении (x-y-1)(x+y+1)=91 . Необходимо проверить, будут ли сами числа и 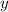в каждом из этих случаев целыми. Можно составить и решить 8 систем, но вместо этого мы составим одну систему в общем виде, решим ее опять же в общем виде и проанализируем результаты.

Рассмотрим систему:

$\begin{cases} x-y-1=A \\ x+y+1=B \end{cases}$

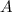Пусть и 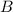- целые числа. Решим систему методом сложения. Сложив уравнения, получим:

2x=A+B

$x=\dfrac{A+B}{2}$

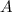Заметим, что является целым числом, когда и 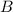имеют одинаковую четность.

Из второго уравнения выразим :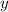

y=B-1-x

$y=B-1-\dfrac{A+B}{2} =\dfrac{2B-2-A-B}{2} =\dfrac{B-A}{2}-1$

Аналогично,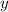 является целым числом, когда 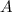и 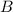имеют одинаковую четность.

Но все числа в наших парах:

$(1;\ 91);\ (7;\ 13);\ (13;\ 7);\ (91;\ 1);\\ (-1;\ -91);\ (-7;\ -13);\ (-13;\ -7);\ (-91;\ -1)$

имеют одинаковую четность. Значит, все 8 систем дадут по одному решению в целых числах. Таким образом, исходное уравнение имеет 8 решений в целых числах.

ответ: 8

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра