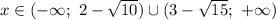|x-6|-|x^2-5x-6|<6 Решите методом интервалов :)

Преобразуем второй модуль и определим нули подмодульных выражений:

Нули подмодульных выражени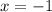й: и 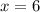, поэтому раскрывать модуль будем на следующих промежутках:

1)

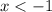
2)

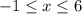
3)

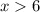
1) Раскрываем модуль на промежутке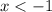 . Первый модуль раскрывается со сменой знака, второй - без смены знака:

Найдем корни соответствующего уравнения:

Методом интервалов найдем решение неравенства:

Учтем условие раскрытия модуля. Для этого сравним числа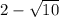 и :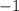

Значит, первое число меньше. Тогда, учитывая условие раскрытия модуля, получим:

2) Раскрываем модуль на промежутке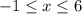 . Оба модуля раскрываются со сменой знака:

Методом интервалов найдем решение неравенства:

Учтем условие раскрытия модуля. Сравним числа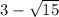 и :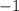

Первое число больше.

Сравним числа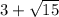 и :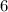

Первое число больше.

Теперь, учитывая условие раскрытия модуля, получим:

3) Раскрываем модуль на промежутке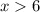 . Оба модуля раскрываются без смены знака:

Используя метод интервалов, запишем решение неравенства:

Число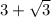 меньше числа .

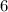Запишем решение, учитывая условие раскрытия модуля:

Итоговое решение неравенства представляет собой объединений трех промежутков:

Упростив запись, получим:

ответ: