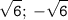X^2-x-1=30/x^2-x. Хелпаните
Другие вопросы по теме Алгебра
Популярные вопросы
- Национальный корпус русского языка (НКРЯ) – это информационно-справочная система,...
2 - Дан равнобедренный треугольник ABC с боковыми сторонами AB=BC. На основании расположены...
1 - Заполните таблицу.Сходства и различия ...
1 - Знаки препинания на месте указанных цифр. Где они необходимы? Объясните. Герой...
2 - 5. Два мальчика на роликовых коньках, оттолкнувшись друг от друга, поехали в...
3 - 10.Какой объем воздуха потребуется на сгорание 56 грамм C8H14? с решением...
1 - Анализ стихотворения малитва...
1 - Составить рассказ рассуждение почему семью можно назвать счастливой...
1 - ИМПЕРИЯЛАР ҚАЛАЙ ПАЙДА БОЛДЫ...
3 - Вопрос по химии Энтальпия какой из приведенных ниже реакций (р, Т = const) равна...
3
D= 1 - 4*1*(-30) = 121
b= -5 не подходит под ОДЗ
ответ:![x_{1,2} = +- \sqrt[]{6}](/tpl/images/1072/6905/faefc.png)
Пусть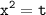 , тогда:
, тогда:
Подставляем:
ответ: