x^2 * log625 (6-x) <= log5 ( x^2-12x+36) 4 вынес в знаменатель x^2, (x^2)/4 в степень, убрал логарифмы и в итоге решал: (6-x)^(x^2)/4 <= (6-x)^2. Можно ли так было сделать, и если нет, то как ? В любом случае решите, хочу свериться со своим ответом

Ответы

Ogents007 15.10.2020 15:18

x∈[-√8;√8] ∪[5;6)

Объяснение:

x² log₆₂₅ (6-x) ≤ log₅( x²-12x+36)

x²-12x+36=(x-6)²=(6-x)²>0

log₆₂₅ (6-x)

6-x>0

-x>-6

x<6

$log_{625}(6-x)=\frac{log_5(6-x)}{log_5625} =\frac{log_5(6-x)}{4} =\frac{1}{4} log_5(6-x)\\\\\ \frac{x^2}{4} log_5(6-x)\leq log_5(6-x)^2; \\\\(6-x)^{\frac{x^2}{4} }\leq (6-x)^2; \\\\esli 6-x1,to\\\\\frac{x^2}{4} \leq 2\\\\x^2\leq 8\\\\x^2-8\leq 0\\\\(x-\sqrt{8} )(x+\sqrt{8} )\leq 0\\\\\\$

x∈[-√8;√8]

если

0<6-x≤1

6-x≤1

-x≤-5

x≥5 тогда

x²/4≥2

x²-8≥0

(x-√8)(x+√8)≥0

тогда

x∈(-∞;-√8]∪[√8;∞),

но поскольку x≥5 и x<6 тогда получаем:

x∈[5;6)

ПОКАЗАТЬ ОТВЕТЫ

deniscv0808 15.10.2020 15:18

$x^2\cdot log_{625}(6-x)\leq log_5(x^2-12x+36)\\\\x^2\cdot log_{5^4}(6-x)\leq log_5(x-6)^2\\\\ODZ:\ \ \left\{\begin{array}{l}6-x0\\(x-6)^20\end{array}\right\ \ \left\{\begin{array}{ccc}x$

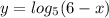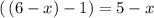По методу рационализации в силу возрастания функции y=log_5(6-x) знак этой функции совпадает со знаком разности $(\, (6-x)-1)=5-x$ .

$(5-x)\cdot \dfrac{x^2-8}{4}\leq 0\ \ \ \to \ \ \ (x-5)(x-\sqrt8)(x+\sqrt8)\geq 0\\\\znaki:\ \ \ ---[-\sqrt8\ ]+++[\sqrt8\ ]---[\, 5\, ]+++(6)\\\\x\in [-\sqrt8\, ;\, \sqrt8\ ]\cup [\ 5\, ;\, 6\, )$