X^2 - 7 < = 0(< = меньше либо равно нулю)
решить неравенство

ответ: [-√7; +√7]

Объяснение:

неравенства решаются методом интервалов))

главное: сравнение происходит с нулем, т.е. нужно определить, где функция принимает отрицательные значения (<0), где положительные (>0), а где равна нулю.

даже если неравенство будет записано так: ,

лучше переписать его в виде: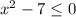 (так меньше шансов наделать ошибок)

следующий шаг:

найти нули (корни) выражения в левой части неравенства-это и есть функция (в нашем случае это ±√7), отметить корни на числовом луче (сколько бы их ни было) и определить знаки этого выражения (функции) на получившихся промежутках...

выбрать нужные промежутки (в нашем случае те, где знак "-")

+++++++++[-√7]---------[+√7]+++++++++>X

ответ: [-√7; +√7]

для неравенства (x-5)(x+1) > 1 рассуждения те же...

сравнивать будем с нулем:

(x-5)(x+1) - 1 > 0

х² - 4х - 6 > 0  найдем корни)) D=16+24=40

корни: x₁ = (4-√40)/2 = 2-√10 и х₂ = 2+√10

+++++++++(2-√10)---------(2+√10)+++++++++>X

ответ: х ∈ (-∞; 2-√10) U (2+√10; +∞)