√x^2-3x+5 + x^2-3x=7 с переменной T; T^2⠀⠀⠀
Другие вопросы по теме Алгебра
Популярные вопросы
- Біліміңді тексер 1. Францияға қарсы күрестің негізгі сатыларын атап...
3 - 37 КЕМ БЫТЬ?В. Маяковский«Кем быть?»1. Знаешь ли ты...Напиши, кем...
1 - ОТВЕТИТЬ НА ВОПРОСЫ Какие виды масс используют в химии? 2. В каких...
3 - f(x) = -x2+2x+81) Графічно зобразити функцію2) Знайти суму цілих...
1 - Из каких материалов кочевники изготовили убранство юрты? Какую информацию...
3 - Петя Костя и Гена нашли 112 грибов. Петя нашёл грибов в 3 раза меньше,...
2 - два творческих и оценочных вопроса по содержанию сказки и ответить...
2 - які дві богині вчинили сварку з приводу хто з них кращий А) венера...
2 - Як я відкрив для себе літературу античності скочно...
3 - Тепловой двигатель совершает за цикл работу а 0.6 кдж при этом холодильнику...
2
Объяснение:
Пусть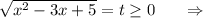
ответ: x₁=4, x₂=-1.