Взаезде на одну и ту же дистанцию участвовали два автомобиля и мотоцикл. Второму автомобилю на всю дистанцию потребовалось на 1 мин больше, чем первому. Первый автомобиль двигался в 4 раза быстрее мотоцикла. Какую часть дистанции в минуту проходил второй автомобиль, если он проходил в минуту на 1/6 дистанции больше, чем мотоцикл, а мотоцикл дистанцию меньше, чем за 10 мин?
Другие вопросы по теме Алгебра
Популярные вопросы
- Великие мечты александра македонского...
1 - Город возле которого персы потерпели поражение от греков...
1 - Дневная норма выработки у рабочего была 15 деталей. на новом станке...
2 - Укажите, что нового появилось в первой половине xix в. в одежде:...
3 - Надо написать 3 предложения,что бы в каждом было по 1 глаголу которые...
2 - :1. 2,5c+1,2+3,6c+5=? 2. 8,8-9,7d-2,5d-3,7=?...
1 - Довжина прямокутника 6см а ширина 3см. знайти площу прямокутника...
2 - Вольтметр показывает 30 в.определить силу тока,протекающего через...
2 - Что такое r в и откуда оно берётся...
1 - Существует мнение, что при тоталитарном политическом режиме гражданское...
2
ответ: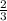
Объяснение:
Пусть первый автомобиль проезжает дистанцию за время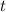 (измеряется в минутах), тогда второй автомобиль проезжает дистанцию за время
(измеряется в минутах), тогда второй автомобиль проезжает дистанцию за время 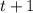 . Поскольку первый автомобиль двигается в 4 раза быстрее мотоцикла, то мотоцикл проходит всю дистанцию за время
. Поскольку первый автомобиль двигается в 4 раза быстрее мотоцикла, то мотоцикл проходит всю дистанцию за время 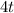 . Поскольку мотоцикл дистанцию менее, чем за
. Поскольку мотоцикл дистанцию менее, чем за 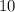 минут :
минут : 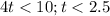
Таким образом, за минуту второй автомобиль проходит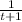 от всей дистанции, а мотоцикл
от всей дистанции, а мотоцикл 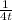
Откуда получаем уравнение:
А значит, второй автомобиль в минуту проходит :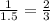 всей дистанции.
всей дистанции.