1. Алгебра
  2. Выясните,при которых значение

Выясните,при которых значение производной функцииf(x) принимает отрицательное значение g(x)=-x/x^2+4

Igrilla19990 Igrilla19990    3   23.02.2022 16:35    1

Ответы
лох251 лох251  23.02.2022 16:40

g(x)=-\dfrac{x}{x^2+4}\ \ ,\ \ \ \ \ \boxed{\ \Big(\dfrac{u}{v}\Big)'=\dfrac{u'v-uv'}{v^2}\ } g'(x)=-\dfrac{x^2+4-x\cdot 2x}{(x^2+4)^2}=\dfrac{x^2-4}{(x^2+4)^2}=\dfrac{(x-2)(x+2)}{(x^2+4)^2}

Решаем методом интервалов Учитывая, что знаменатель будет положительным при любых  х , знак производной зависеть будет только от числителя.

Знаки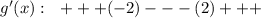  g'(x):\ \ +++(-2)---(2)+++

Выбираем знак минус,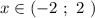   x\in (-2\ ;\ 2\ )  .

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
123KETCHUP123 123KETCHUP123  23.08.2019 04:40
Разложить на множетели 5ab-15b-5a+15...
weldys99 weldys99  23.08.2019 04:40
Корнями квадратного уравнения x^2+vx+n=0 являются −12 и 1. чему равны коэффициенты v и n? (первым впиши наибольший коэффициент) ответ: v = n =...
aish17 aish17  23.08.2019 04:40
Сполным решением 1)m+n/3x + 3m-n/3x 2)a+2b/5b - 2b-a/5b 3)x+4y/4a^2 + 3x-2y/4a^2 4) 15m-6n/y^4 - 9m-n/y^4 /-это дробь...
bataev2007 bataev2007  23.08.2019 04:40
Разложить на множители выражение: а) p(a+b)-a-b; б) c(x+y)+7x+7y; в) ma+6m-3a-18....
amdv amdv  23.08.2019 04:40
Решите графически уравнение 4/х=х/2 - 1. я просто не помню графики...
fobose1123 fobose1123  11.06.2019 00:10
Умаши5 яблок подруге она отдала 2 сколько у нею осталось...
aigerka19 aigerka19  11.06.2019 00:10
Решите неравенство 3x^2-13x+12 0...
kilu558028 kilu558028  11.06.2019 00:10
Решите ! на стороне cd квадрата abcd лежит точка р такая, что ср=pd , о- точка пересечения диагоналей. выразите векторы во, вр, ра через векторы х= ва и у= вс...
gulnoza10 gulnoza10  11.06.2019 00:10
Не выполняя вычислений определите знак результата (-1)в 5 степени*(-2)в 10 степени*(-3)в 15 степени еше 1 вычислите 8+7в 2 степени,(8+7)в 2 степени,8во 2 степени+7 во...
КРЕНДЕЛЬ228 КРЕНДЕЛЬ228  11.06.2019 00:10
Вычислите: 15,7*3,09+15,7*2,91; 4,03*27,9-17,9*4,03....

Популярные вопросы