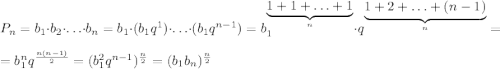Выведите формулу произведения первых n членов прогрессии
Другие вопросы по теме Алгебра
Популярные вопросы
- . Прочитайте текст і надпишіть над кожним займенником його відмінкову форму. Завершіть...
1 - До іть будьласка, на кону життя та смерті стою. Дуже потрібна до , благаю...
3 - В чем схожества и различи однояйцевых ?...
1 - Полый шар равномерно заряжен. В центре шара потенциал 100 В, а на расстоянии 30...
1 - ответить на вопрос Він був високий і худий, і чоло в нього високе. У реченні є...
2 - Паспорт твору Свиня свинею Руданського...
2 - 1I don’t like ___ up late on Sunday. a get b gets c getting d got 2___ skateboarding...
3 - Синтостически разбор:Юноша был одет в кожаную куртку...
3 - 5. Установіть відповідність між поняттями та їх характеристокою. 1. Фосфорилювання....
2 - точка аведал говорит толщины А на 6 см по Heli AC и AB утолите сплошную а кут 45°...
3
k-ый член прогрессии выглядит так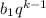 , где q - знаменатель прогрессии.
, где q - знаменатель прогрессии.
Необходимо найти