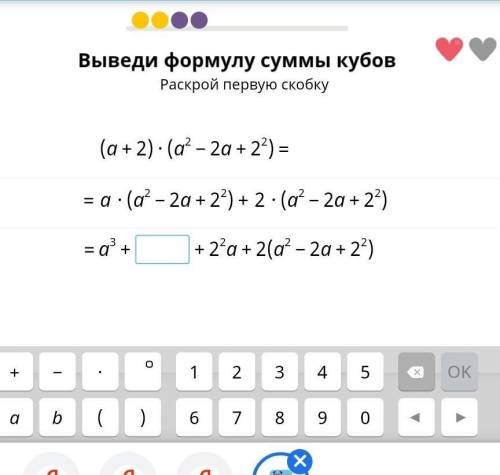
Выведи формулу суммы кубов (на фото)
Другие вопросы по теме Алгебра
Популярные вопросы
- Сочинение на тему ,,осень любимая пора пушкина,,...
2 - Поезд подходит к станции тормозит с ускорением -0,5м с определите тормозной...
3 - Найти натуральные числа,образующие арифметическую прогрессию, если произведение...
2 - Обед богатого и бедного в новое время (просто перечень еды)...
1 - Какая питьевая вода распространена по городу вологда и какой лучше приобрести...
3 - Відредагувати речення . у касі є проїзні білети на всі види транспорту....
2 - Курсы иностраных языков посещает 100чел, язык изучает в 2 раза больше чел...
1 - Значение пиявок в 1) природе 2) в жизни человека обязательно два пункта...
2 - Составьте предложения использую глаголы в соответствующей форме 1.carlos/study/history...
1 - Составить по : m=0,4кг; дельта t=50 градусов; q=78кдж...
2
1² + 2² + 3² + ... + n² = n * (n + 1) * (2n + 1) / 6.
Теперь давайте рассмотрим данное изображение сосуда, заполненного кубиками.
Мы видим, что есть n слоев кубиков. Первый слой состоит из 1^3 = 1 кубика, второй слой из 2^3 = 8 кубиков, третий слой из 3^3 = 27 кубиков и так далее. Общее количество кубиков будет равно сумме чисел от 1 до n возведенных в куб.
Таким образом, сумма кубов чисел от 1 до n будет выглядеть следующим образом:
1^3 + 2^3 + 3^3 + ... + n^3.
Для удобства дальнейших вычислений мы можем воспользоваться формулой суммы квадратов, введя переменную k, которая будет равна k^2 и выполнять роль числа, возведенного в куб. Тогда наша формула будет иметь вид:
k^2 = (k * (k + 1) * (2k + 1)) / 6.
Теперь давайте переведем обратно к нашей изначальной переменной n. Заменим k на n и получим искомую формулу:
1^3 + 2^3 + 3^3 + ... + n^3 = (n * (n + 1) * (2n + 1)) / 6.
Таким образом, мы получили формулу суммы кубов чисел от 1 до n.