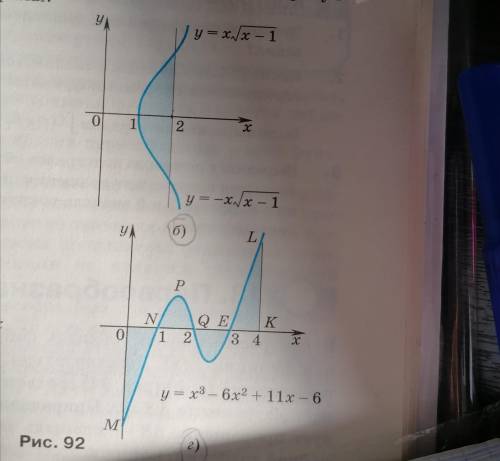
Выразите площади фигур изображенных на рисунке 92 через интегралы

Для вычисления площадей фигур на рисунке 92 с использованием интегралов, мы должны разделить каждую фигуру на более простые геометрические формы, для которых мы знаем формулы для вычисления площадей. Затем мы можем использовать интегралы для вычисления суммарной площади всех этих форм.

1. Фигура А:
Плоская фигура А состоит из двух частей: прямоугольника и треугольника.
- Площадь прямоугольника: чтобы вычислить площадь прямоугольника, мы умножаем его длину на ширину. На рисунке нет явных размеров, но предположим, что длина прямоугольника равна a, а его ширина равна b. Тогда площадь прямоугольника равна ab.
- Площадь треугольника: для вычисления площади треугольника мы можем использовать формулу 1/2 * основание * высота. В данном случае, основание треугольника равно b, а его высота равна а. Таким образом, площадь треугольника равна 1/2 * ab.

Суммарная площадь фигуры А равна площади прямоугольника плюс площади треугольника: ab + 1/2 * ab = 3/2 * ab.

2. Фигура B:
Фигура B также состоит из двух частей: прямоугольника и треугольника.
- Площадь прямоугольника: предположим, что длина прямоугольника равна c, а его ширина равна d. Тогда площадь прямоугольника равна cd.
- Площадь треугольника: основание треугольника здесь равно d, а его высота равна e. Таким образом, площадь треугольника равна 1/2 * de.

Суммарная площадь фигуры B равна площади прямоугольника плюс площади треугольника: cd + 1/2 * de.

3. Фигура C:
Фигура C - это просто круг с радиусом f. Площадь круга вычисляется по формуле πr^2, где π - математическая константа, приближенно равная 3.14159, а r - радиус круга. Таким образом, площадь фигуры C равна πf^2.

Таким образом, площадь фигур на рисунке 92, выраженная через интегралы, будет:
Фигура А: 3/2 * ab
Фигура B: cd + 1/2 * de
Фигура C: πf^2

Примечание: Поскольку размеры фигур на рисунке не были указаны, я использовал символы a, b, c, d, e и f для обозначения неизвестных размеров. В реальной задаче необходимо использовать известные числовые значения этих размеров для подсчета конкретных численных ответов.