Выражения 1) (x+3//x-3)+(9/x²-3x) 2) (b+c/b²-/b²-c²-c/b²+bc) 3) (1/x-/x³-8)+(x-2/x²+2x+4)
Ответы
Если 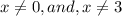 , то:
, то:
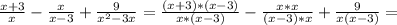
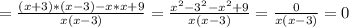
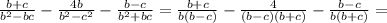
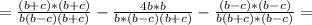
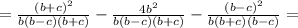
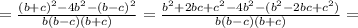
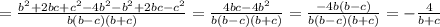
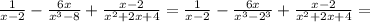
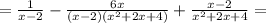
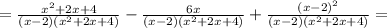
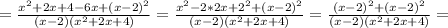
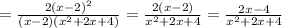
ПОКАЗАТЬ ОТВЕТЫ
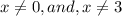 , то:
, то: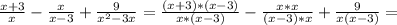
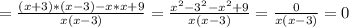
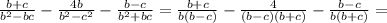
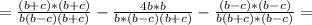
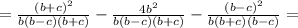
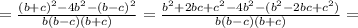
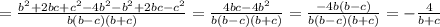
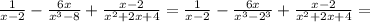
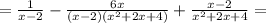
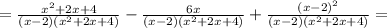
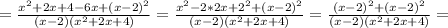
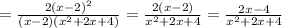
Другие вопросы по теме Алгебра
Популярные вопросы
- Первая бригада может выполнить за 16 ч а вторая за 48 за сколько часов совмесной...
3 - Впараллелограмме аксм угол с равен 120° ск равен 6 см ак равен 8 см найдите площадь...
3 - 1)вычислите объем и площадь поверхности куба с ребром 2см. 2) длина прямоугольного...
3 - Решить показательное неравенство 0,5^2x-1 ≥ 0.125...
2 - Сочинить небольшой рассказ про антонимы по языку (только брать не из ! . )...
1 - Выпиши с маленькой буквы прилагательные, разряд которых определён правильно, и...
2 - Найти последние пять цифр ответа 14^(2^2015)=...
3 - Составить словосочетание наречие+глаголы 10 слов. ! )...
3 - Примеры слов с переносным значением. примеры ононимов....
1 - Определить ( по фенотипу и генотипу) потомство полученное при скрещивании двух...
2