Выражение: 1) a-15\4a-20 - a-5/4a+20 + 30\a²-25; 2) 8a³+100a\a³+125 - 4a²\a²-5a+25. ! нужно !
Другие вопросы по теме Алгебра
Популярные вопросы
- Маляр за 1ч может окрасить стену площадью 8,4 м2, а маляр-стажер...
3 - Алеша попович сказал:У змея горыныча больше 3 голов Добрыня сказал:У...
1 - Установите соответствие между графиками функций и формулами,...
1 - Расставить коэффициенты методом электронного баланса в уравнении...
3 - Куаныш в бокал с чаем положил кусочек сахара-рафинада, а Антон...
2 - Почему КПД реальной машины меньше КПД идеальной машины?...
2 - Контрольная работа Двусоставное предложение 1. Выпишите все словосочетания...
1 - самостоятельная по биологии...
3 - Вміст солі в морській воді становіть 5%. Скільки кілограмів прісної...
2 - Найдите область определения функции Задан Ной  Формулой a)y=;x-6...
3
Объяснение:
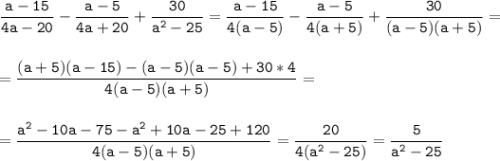
**************************************************