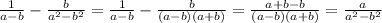Выражение: 1) 2/3-a+a^2-4/a^2-9*a+3/a-2 2)ab/a^2-b^2: ab/a+b-b/a^2-b^2 п.с. / дробная черта, a^2 а во 2 степени, * умножение, : обычное деление !
Другие вопросы по теме Алгебра
Популярные вопросы
- ответьте даю 35 звоздочек...
1 - Завдання 1. Дай характеристику природного комплексу ( парк « Ювілейний»...
1 - (сделай разметку) 67-x=100...
1 - .Подготовить сообщение по теме Урок Памяти и Славы. Парад Победы....
3 - Реши уравнение x в квадрате равен 400...
2 - Чи був розкол ОУН неминучим?...
1 - Хто з правителів давав настанови своїм дітям?...
2 - Композитор, создатель жанра концертного этюда: а)Ф.Лист. б)Ф.Шуберт....
1 - Морф. разбор местоимения Найди местоимение в предложении: Родители...
3 - У выражение: а) (2х + 1)2 + (3х - 1)(3х + 1); б) (с + 3)3 – (с +...
3
1)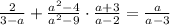
1)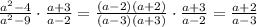
2)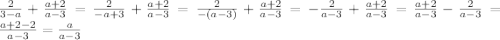
2)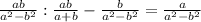
1)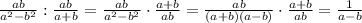
2)