1. Алгебра
  2. Выполнить действия 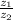, z₁³ в тригонометрической

Выполнить действия \frac{z_1}{z_2}, z₁³ в тригонометрической форме с числами z₁=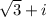\sqrt{3} +i, z₂= -3-3i.

anasgaliev anasgaliev    3   16.06.2020 20:00    0

Ответы
arsenagadzhanin arsenagadzhanin  19.08.2020 01:53

Переведем числа в тригонометрическую форму:

z_1=\sqrt{3} +i

|z_1|=\sqrt{(\sqrt{3} )^2+1^2} =2

\arg z_1=\mathrm{arctg}\dfrac{1}{\sqrt{3} } =\dfrac{\pi}{6}

\Rightarrow z_1=2\left(\cos\dfrac{\pi}{6} +i\sin\dfrac{\pi}{6} \right)

z_2=-3-3i

|z_2|=\sqrt{(-3)^2+(-3)^2} =3\sqrt{2}

\arg z_2=\mathrm{arctg}\dfrac{-3}{-3}-\pi=\dfrac{\pi}{4} -\pi=-\dfrac{3\pi}{4}

\Rightarrow z_2=3\sqrt{2} \left(\cos\left(-\dfrac{3\pi}{4}\right) +i\sin\left(-\dfrac{3\pi}{4}\right) \right)

Для деления используется следующая формула:

\dfrac{z_1}{z_2} =\dfrac{\rho_1}{\rho_2} \left(\cos(\varphi_1-\varphi_2)+i\sin(\varphi_1-\varphi_2)\right)

\dfrac{z_1}{z_2} =\dfrac{2}{3\sqrt{2} } \left(\cos\left(\dfrac{\pi}{6}-\left(-\dfrac{3\pi}{4}\right)\right)+i\sin\left(\dfrac{\pi}{6}-\left(-\dfrac{3\pi}{4}\right)\right)\right)

\dfrac{z_1}{z_2} =\dfrac{\sqrt{2}}{3 } \left(\cos\left(\dfrac{\pi}{6}+\dfrac{3\pi}{4}\right)+i\sin\left(\dfrac{\pi}{6}+\dfrac{3\pi}{4}\right)\right)

\dfrac{z_1}{z_2} =\dfrac{\sqrt{2}}{3 } \left(\cos\left(\dfrac{2\pi}{12}+\dfrac{9\pi}{12}\right)+i\sin\left(\dfrac{2\pi}{12}+\dfrac{9\pi}{12}\right)\right)

\boxed{\dfrac{z_1}{z_2} =\dfrac{\sqrt{2}}{3 } \left(\cos\dfrac{11\pi}{12}+i\sin\dfrac{11\pi}{12}\right)}

Для возведения в степень используется следующая формула:

z^3=\rho^3 \left(\cos3\varphi+i\sin3\varphi\right)

z_1^3=2^3\left(\cos\left(3\cdot\dfrac{\pi}{6}\right) +i\sin\left(3\cdot\dfrac{\pi}{6}\right) \right)

\boxed{z_1^3=8\left(\cos\dfrac{\pi}{2} +i\sin\dfrac{\pi}{2} \right)}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ника2762 ника2762  05.09.2019 22:25
1/9а²+1 1/3а+4 разложите на множители выражение .)...
ed31121 ed31121  05.09.2019 22:25
Log 729 по основанию 2log 9 по основанию 2​...
fyjdtjjhtjh fyjdtjjhtjh  05.09.2019 23:00
Найдите границу относительной погрешности двух приближённых значений чисел а = 7,360 (плюс минус) 0,004 и b = 8,610 (плюс минус) 0,005. и абсолютную погрешность их суммы....
fariii046 fariii046  05.09.2019 23:00
Цена на картофель в связи с плохой погодой повысилась на 30%. через некоторое время цена картофеля понизилась на 30%. когда картофель стоил дороже , до повышения цены или...
LiliLay17 LiliLay17  05.09.2019 23:00
Можете решить: 0,2х+3,4=0,6х–2,6; 3х(4х–1)–6х(1,5+2х)=4,8; (х–8)2–х(х+6)=–2...
Arra1234566 Arra1234566  13.01.2020 08:02
Представьте в виде произведения двучлен: 1)c²-0,49 2)16-k² 3)400-m² 4)t²-225 5)1,69-b² 6)y²-16/81 7)25x2-4 8)25/36-64y²...
рита461 рита461  13.01.2020 08:09
Коробку із кришкою, що має форму прямокутного паралелепіпеда, довжи-на якого 8 см, ширина — 5 см, а висота — 4,5 см, обшивають матерією. зна-йдіть площу матерії, якщо на...
biksummer23 biksummer23  13.01.2020 08:09
2x - 10x = 0.2 + 6x = 0. 2 4x2 + 20x = 0. 3x2 - 12x = 0.2 2x3+ x = 0.24. x - x = 0. 3x2 - 27 = 0. 2x2 - 32 = 0. 4x3 + 20x = 0. 2 3x - 12x = 0.​...
ilmir14 ilmir14  13.01.2020 08:22
Цифра, стоящая в разряде десятков двузначного числа, на 2 больше цифры, стоящая в разряде единиц. если это число умножить на сумму ее цифр, то получается 900. нужно это двузначное...
Savcik Savcik  13.01.2020 08:28
Решить 1-ю .вычислите неопределённый интеграл...

Популярные вопросы