Вычислите
[tex]a=tg^{2}36^o*tg^{2}/tex]
оч !
Другие вопросы по теме Алгебра
Популярные вопросы
- Мой ответ3. Қазақстанның көршілес елдермен байланысын сипаттаңыз....
2 - 6 класс тест Французский язык...
3 - Длинным клювом разобрать слова как части речи...
3 - Кустарга камкорлык ангиме курау...
2 - На одном участке посеяли 383 ц ячменя, а на другом — 398 ц. С первого участка...
2 - Менин дағыстаным шығармасында көтерілген басты мәселе қандай?...
1 - Проанализируйте приведенные высказывания. Какие из них верны, а какие – нет?...
3 - Нужно сделать полностью задание, а не частью Задание с развёрнутым ответом...
1 - Қтапсырма. Мәтіндегі көтерілген мәселені әлеуметтік қажеттілік тұрғы-онан...
1 - В треугольнике ABC (см. рисунок) BC = 14, sin A = , внешний угол при вершине...
2
Вначале понизим степени тангенсов, переходя от них к косинусам двойных углов:
Далее в числителе и знаменателе раскроем скобки:
К произведению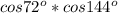 применим теперь трюк "гармошка", а к сумме
применим теперь трюк "гармошка", а к сумме 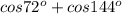 - трюк "домино":
- трюк "домино":
Таким образом,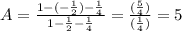
ответ: 5